252(1)

Przy układaniu równania różniczkowego dla danego zadania w postaci związku pomiędzy różniczkami zmiennych wolno czynić rozmaite założenia upraszczające zadanie i nie wpływające przy tym na jego wynik. Wolno np., podobnie jak to się czyni przy wyznaczaniu różniczki niewiadomej wielkości (rozdz. V, § 3), niewielki kawałek krzywej traktować jako odcinek prostoliniowy, a niewielki kawałek (płat) powierzchni traktować jako płaski, w ciągu małego odstępu czasu wolno ruch zmienny rozpatrywać jako jednostajny i analogicznie przyjąć, że każdy proces fizyczny, chemiczny czy techniczny przebiega ze stałą prędkością.

Przy układaniu równania różniczkowego dla danego zadania jako związku pomiędzy pochodnymi uwzględnia się sens geometryczny, fizyczny lub mechaniczny pochodnej (rozdz. Tf, § 1. 1 i 12, 14, 15).

Prócz tego, układając równanie różniczkowe zadania w zależności od jego warunków, uwzględniamy znane prawa fizyki, chemii i mechaniki lub też innych nauk i różne zależności matematyczne.

1162.    Jaka krzywa ma tę wiasność, że odcinek dowolnej stycznej do niej, zawarty między punktem styczności a osią odciętych, jest dzielony osią rzędnych na dwie równe części.

Rozwiązanie: Równanie stycznej do szukanej krzywej w dowolnym jej punkcie (x,y) będzie miało postać Y—y — y'(X— x), gdzie X, Y są współrzędnymi dowolnego punktu na tej stycznej (rozdz. II, § 11).

Podstawiając do równania stycznej wartość Y = 0, znajdujemy odciętą X₀ punktu, w którym styczna przecina się z osią Ox: X_a = x— y-.

Z warunku zadania wiemy, że X₀+x — 0, czyli 2x—~ = 0.

Rozwiązując otrzymane równanie różniczkowe dla szukanej krzywej jako równanie o zmiennych rozdzielonych, otrzymamy

2-^- = —-; 2in j v] = ln |jr|-|-lnC; y¹ — Cx

Wobec tego szukaną krzywą jest parabola o wierzchołku w początku układu, symetryczna względem osi Ox (dokładniej jest to niejedna parabola lecz rodzina parabol).

1163.    Jaki kształt powinna mieć jednorodna pionowa kolumna o przekroju kołowym, ażeby naprężenia, wywołane w poziomym przekroju poprzecznym (czyli nacisk działający na jednostkę pola powierzchni przekroju) na skutek działania ciężaru P podtrzymywanego tą kolumną i jej własnej wagi, było wszędzie jednakowe (kolumna stałego naprężenia)? Ciężar właściwy materiału kolumny wynosi fi, a promień górnej podstawy wynosi r.

Wyznaczyć następnie, przy jakich promieniach górnej i dolnej podstawy filaru mostu naprężenie w każdym jego przekroju poprzecznym (poziomym) będzie wynosić 3 000 kG/dcm², jeżeli ciężar właściwy materiału filaru wynosi 2.5 kG/dcm³, jego wysokość 12 m, a podtrzymywany ciężar 90 000 kG.

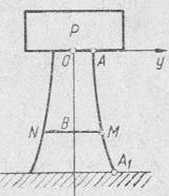
Rozwiązanie. Niech przekrój pionowy kolumny przechodzący przez jej oś symetrii ma kształt przedstawiony na rys. 216.*

♦x

Rys. 216

Obierając zgodnie z rysunkiem układ współrzędnych \Oy, przetnijmy kolumnę poziomą płaszczyzną, przechodzącą przez dow olny punkt A/(.v, y) szukanej krzywej AA_lt i określmy, jakie naprężenie wytwarza ciężar P oraz własny ciężar górnej odciętej części kolumny w przekroju poziomym MN (naprężenie to. jak wiemy, będzie równe sile wypadkowej działającej na jednostkę pola powierzchni tego przekroju).

Objętość górnej odciętej części kolumny, jako objętość bryły powstającej z obrotu trapezu krzywoliniowego OAMB przylegającego do osi Ox dookoła tej właśnie osi (rozdz. V, § 5), wyraża się całką

.V

V = rr | yV.v <>

a ciężar jej wynosi G = fiV.

Dzieląc całkowity ciężar P\G przez pole S = rrr przekroju MN, otrzymamy naprężenie dla tego przekroju. Z warunku zadania wiemy, że naprężenie to jest niezależne od przekroju i że dla każdego przekroju ma tę samą wartość.

507