mech2 171

340

340

A1

=    = u) 1 sin tp ,

^BA1 " ^BA2

m w 1 sin tp.

Są to odśrodkowe siły 'bezwładności skierowane prostopadle do osi obrotu. Jeżeli nie można pominąć rozmiarów suwaka, to do każdej jego cząstki należy przyłożyć siłę bezwładności

Po przyłożeniu sił bezwładności, nadajemy układowi przemieszczenie przygotowane ó <p w kierunku zgodnym z ruchem wskazówek zegara. Korzystamy z o-gólnego równania dynamiki układu

6A (F) + ÓA (b) = 0.

Wyznaczamy prace przygotowane poszczególnych sił:

6 A    = -G^l sintp ócp = -mgl Bintp 6 tp ,

G₂1 sincp ótp = mgl sintp 6 <p ,

⁶* (\l) * W cos q> ótp = m to ^1 sin tp cob tp 6 cp , = B_a21 cob qp ótp = m to 2i2

sin (p cos tpó <p ,

^{5 A} sp^żyny) = “° (9 - <P^) ⁶ %

óA Ca

6 A

os>

G-j 6 z,

przy czym

z = 21 cob tp ,

6 z = -21 sin tp 6 tp ,

czyli

6 A f = -21G,. sintp 6<p = -21m_c g sin tp6 <p .

Praca sił bezwładności B„. Buwaka jest równa zeru, ponieważ przemieszczenie

Cii.

przygotowane 6z jest dla każdego elementu suwaka prostopadłe do kierunku siły bezwładności,

Podstawiając do ogólnego, równania dynamiki otrzymamy:

/ n    2    2    2    2

6 A ( F / + 6A f BJ = mto 1 sintp coscp ótp + m to 1 8in tp coBtpó tp -- c (p - tpj^ó tp - 21m_c gBintp 6 cp= 0,

stąd prędkość kątowa

■i

-;-n

2glm_c Bintp+ c£cp - <Pq)

ml ein2 cp

Zadanie 4 (rys. 252)

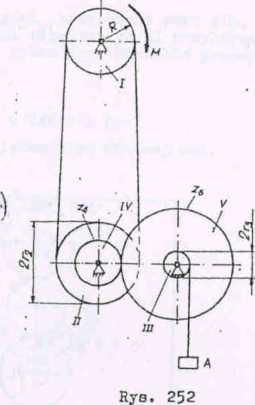
Na bęben napędowy I podnośnika działa stały moment obrotowy M. Określić przyspieszenie podnoszonego ciężaru A. Ciężary części obracających się, ciężary lin oraz tarcie pominąć. Dane są: promień E bębna I, promienie bębnów II i III odpowiednio równe rj i n, przełożenie między kołami IV i Y z,-/z, = ^ oraz masa m ciężaru A.    04

Odp.

- g.

Mr₂k

mEr_

Zadanie 5 (rys. 253)

Na trzech pełnych jednorodnych. wałach znajduje Bię belka o masie m₂, a każdy z wałów jest napędzany momentem obrotowym M. 0-kreślić przyspieszenie belki, jeśli jest dana masa nkażdego z wałów, promienie r wałów, a między wałami i belką nie ma poślizgu. Tarcie w OBiach pominąć.

Odp.

6M

(3m₁_+ 2m₂) r

Zadanie 6 (jtyb. 254)

Reduktor składa się z dwóch kół zębatych i II, których masy wynoszą odpowiednio nb| IH2, a promienie r i R. Na pierwsze koło

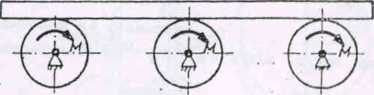
Rys. 253

i

działa moment M, wprawiający je w ruch, a na drugie koło działa moment hamujący K₂ = 3/4 MiOkreślić przyspieszenia kątowe i e₂ kół,traktując je jako jednorodne tarcze i przyjmując R = 12r«-Tarcie w łożyskach pominąć.

Odp.

8r

15M

(^Bi^ł ”2)

E_ =

32r

5M

C^mi ⁺ “2)

Zadanie 7 (rys. 255)

Regulator w postaci dźwigni kątowej ma zamocowane na końcach Ai>A₂ ciężary o jednakowych masach. Długości ramion dźwigni wynoszą I4 i 1₂ Q&k na rys. 255), przy czym l«i / 1₂, kąt między ramionami wynosi 90°.Pomijając masę dźwigni oraz tarcie określić przy jakiej prędkości kątowej regulatora prosta łącząca' środki ciężarów ustawi się poziomo.

4