mech2 104

^r

206

Oststeoznie otrzymujemy

2 sin uj t + r_Q,

_r2 _    .X.    .    _2

2Q w

sin w fc.

■l/*l * ^

V ⁰ 2Q (ł)

Zadanie 8 (rys. 1^8)

Pręty OA i AB wirują wokół osi pionowej przechodzącej przez'punkt o z prędkością kątową w, pozostająo w jednej płaszczyźnie pionowej i tworząc z osią odpowiednio Kąty a i p . Długości prętów wynoszą 1.,    1

masy , m₂. ffyznaozyć kręt względem osi obrotu.    '

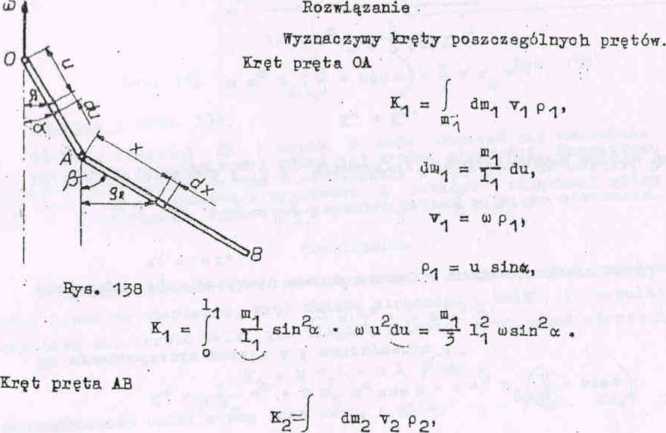
^m2

®p

dm₂ = dx, v_{2 s} <u p ₂,

P₂ = 1^ sina + x sin p , b

C    2

£₂ =    (1^ sina > x sinp) a) dx,

o ^

K₂ = ®2 m (ł^ sin^a + l,jl₂ ^s^-^{na a}^ⁿ P + l| sin^ p ).

l

I

l

i h

Zadanie 10

Po obwodzie poziomej tarczy o promieniu r i masie ta mogącej odrsr-_oać się bez taroia dookoła pionowej osi,zaczyna poruszać się punkt o ma-

‘ ’ ” ^{i j} - •’-*-*—- — ^T-’— — ¹—^A----^J---•*---pun-

o

i# I'®

i s

-■$&

207

:^_ręt układu Jest sumą krętów poszozególnyah ozęści

S&

+ K₂ = u

'Np 2

\-j- + m ₂) 1₁ sin a + m^^l^sin a sin|3 +

1^ sin^3

Zadanie 9

Na szale wagi, z których, każda waży Q, spadły jednocześnie ciężary

...... ~    ć    ‘ '

i-n i 0^ s wysokości h. i

• ^    (^ ys- ^ yĘ>

2*

Wyznaczyć początkową prędkość szal.

Odp.

v =

+~^ '+^2

_gia m-i ze Btałą prędkością liniową ■y^.Jaka powinna być masa drugiego ktu,który jednocześnie zaczyna poruszać się po współsrodkowym okręgu promieniu ze stałą prędkośoią liniową V2, aby tarcza pozostała w spc— •o zynku.

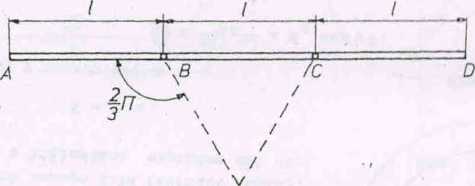
Zadanie 11 (rys. 159)

Trzy jednakowe pręty JLB, BC i CD o długości 1 każdy, połąozone zawiasami nie dająoymi tarcia, poruszają się ruahem postępowym z prędkością v po gładkiej płaszczyźnie poziomej tnorząo linię prostą prostopadłą do tej prędkości. Po jakim czasie spotkają się końce prętów skrajnych, gdy zatrzymamy środek pręta środkowego.

_n, .    4 u 1

Odp. t = -n-v •

Rys. 159.

5.5. Dynamika ruchu postępowego Zadanie 1 (rys* 140)

Wózek o ciężarze Q należy wciągnąć po równi nachylonej do poziomu pod kątem _a na wysokość h. Obliczyć jaki oiężar G należy zawiesić na drugim końcu liny ciągnąoej wózek,by wciągnięcie odbyło się w ozasie t^. (Krążek, przez który jest przerzucona lina traktować jako nieważki,a tarcie w krążku i opór toczenia pominąć.)

ll