skanuj0021 (17)


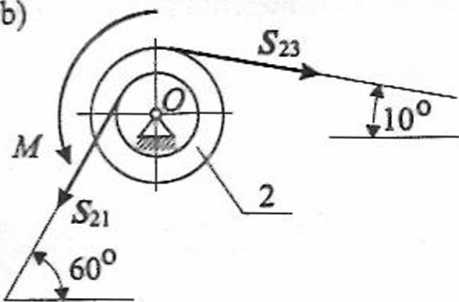
po uwzględnieniu zależności (D-18.5), (D-18.35) i (D-18.36) w równaniu (D-18.34) otrzymamy
= [G, sin 60° - 7j-Su]-il + [-G]cos60°+N]]jl. (D-18.37)
Po pomnożeniu skalarowo, równania (D-18.37), przez wektory'jednostkowe i] i jv otrzymamy dwa równania
m,= G, sin 60° - 7j - Sn, (D-18.38)
0 = -G] cos 60° + W,. (D-18.39)
Po uwzględnieniu zależności (D-18.10) i (D-18.11) w rówmaniu (D-18.38) będziemy mieli
m,*) = Sj02 ~Si2- (D-18.40)
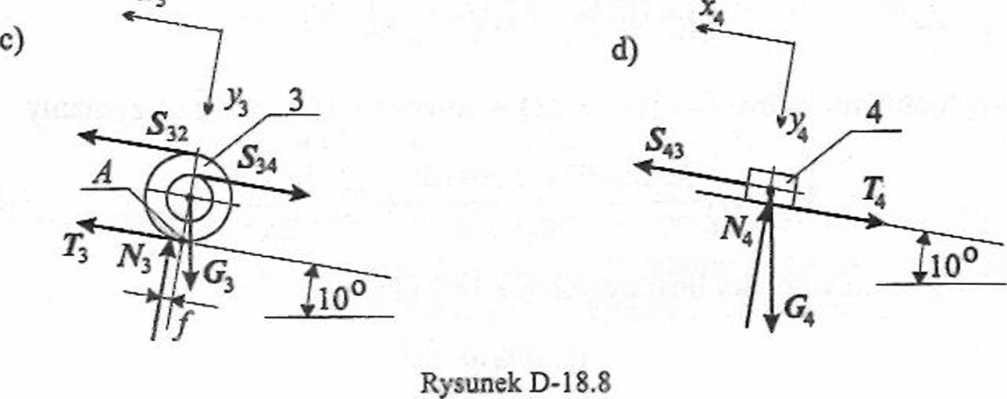
Dla ciała 4 (rys. D-18.8d) - druga zasada dynamiki przyjmie postać
m4a4 =G4 + Ar4 +Tą +S43, (D-18.41)
228
Wyszukiwarka
Podobne podstrony:
skanuj0019 (22) Po uwzględnieniu, że a3 = 0, drugą zasadę dynamiki (D-18.1) można zapisać G3 + N3+T3
480 (7) 4gQ 12. Prądy i tkktromignetyuny moment obrotowy maszyny indukcyjnej a po uwzględnieniu zale
Strona0054 54 Po uwzględnieniu zależności (2.108) i (2.103) otrzymano zatem: 54 x = Cx cos co0t + C2
558 2 15. NOWE ŹRÓDŁA I TECHNOLOGIE WYTWARZANIA ENERGII ELEKTRYCZNEJ Po uwzględnieniu zależności
przeto(10.22) Wzmocnienie układu ze sprzężeniem zwrotnym (10.23) po uwzględnieniu zależności
258 (9) Okazuje się, że po uwzględnieniu zależności X = X° uzyskuje się takie same wartości wyrównan
skanuj0022 (17) gdzie a4 =*4*4> (D-18.42) £43=S43/4, (D-18.43
wnikanie rurociąg c) wnikania ciepła na zewnątrz rurociągu: R a2 (3.19) Po uwzględnieniu oporów ciep
skanuj0017 (24) stąd otrzymamy N} = G] cos 60°, r, =/iiVj =/iGjCos60o. (D-18.10) G
image 020 20 Parametry anten Zależność (1.17) można zapisać w postaci: (1.18) D 47
skanuj0402 — dla hamulca różnicowego (15.18) P _ Fi ‘ ^2 F2 a l dla hamulca sumowego zostaje zacho
skanuj0402 — dla hamulca różnicowego (15.18) P _ Fi ‘ ^2 F2 a l dla hamulca sumowego zostaje zacho
41190 skanuj0017 (24) stąd otrzymamy N} = G] cos 60°, r, =/iiVj =/iGjCos60o. (D-18
015 5 Po wykorzystaniu zależności (1.4), (1.5), (1.6) oraz (1.14) i przekształceniach (1.18) (k - 1)
więcej podobnych podstron