mechanika109

i 2 , cosa .

= I -co*A - sina e_v

^T sina ' *

a =■ e x r =

O

o> * ctg a O O

A tg a A cos a A sin a ♦ oJ/jctga cosae_c = A cos a e_v + o>*Acosa ctga e.

a_A - 10 x v =

	^e> ^e«
0	-w* ctga 0
-w* A cos a	0 <ołA

- -co*Actga -e_x - oj!, A cos a ctga *e_?

mm    mm    mm    J    __    ^    —

a = a_B = a_o + a_d = -w^Aclga-e^ ti>*Acosa-c

Zadanie 2.30

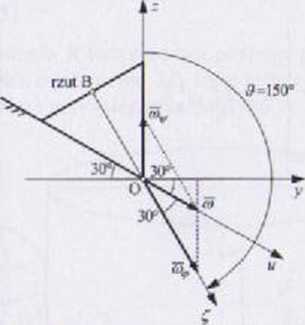
Stożek ruchomy toczy się bez poślizgu po stożku nieruchomym. Okres obrotu własnego wynosi 7^. a wysokość stożka ruchomego wynosi A. Wyznaczył prędkość i przyspieszenie punktu B w chwilowej konfiguracji układu.

Rozwiązanie

Ruch stożka spełnia warunki precesji regularnej. Chwilowa oś obrotu pokryun się z krawędzią styku stożków. Zwroty wektorów <ó_t. u>_ę wynikają / za/n.i czonego kierunku toczenia się stożka.

Kinematyka 2.2 5. Precesja regularna ciała .sztywne*

__JL -___ M _ J

i ił>, cos60^D = — oj >0,    (*>. - (ił* - oj sin 60° = oj,, — u> < 0

-A. <

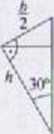
Inlc/nośo geometryczne:

h	r r*r\r* TH" _w.	h =	* - ^2 h
b			cos 30° ^
f	- sin 30° =>	C =	A sin 30“ - -A
h			2
,1	- cos30° =>	d -	A cos 30“ -
			2
f >	OB* = - e -	cev ♦	de. » — he - -
	2 *	z	^! f '

Ae.

|Vyznaczenie wektorów u, e: 2r.

he.

(j - G>_ye_r + <u.e.

▼    ^,m) T    r    w

u

M

' tg30^c

fi Ha * - ~ tl>	- jff-i.
W 2 •	3 2
li to, e =	^Gii
r» * •:	3 * ^1 2
1 - uj^ cos60^3 w

“ **> *g30°

li.

■i-#.

fi

<*>♦ = ^v3 <*\

e, = -<o_e„ - —(j_e *^T 2

«p r

i

lirm.iiyku. 2.2.5 Precesja tytularna ciała s/tywnego

219

1

- [fi    y^l -    1    -    fi -

2

(»i ♦ (ił^    ■    — w.e „ + ---- we,    =    -o> e    - —u> e

3

• ^f    2 ♦ > I 3    2 I * ¹    2 *    6 * ^z