mechanika70

Ruch krzywoliniowy punktu na płaszczyźnie opisuje się we współrzędny tli kartczjaiiskich. biegunowych lub naturalnych.

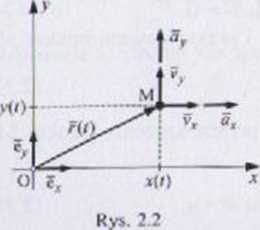
Układ współrzędnych kartezjańskich xy, rzuty wektora prędkości ńł) i przyspieszenia a(t) pokazano na rys. 2.2. Współrzędnymi ruchu punktu s* funkcje x{t), y(t). Wektory r(t), v(f), a[t) oraz ich moduły wynoszą

'■(O = v'*²(0 ⁺y²(/)

7(t) = x(t)e_x ♦ y(r)e_y* v{t) = r[t) = x(t)e_t +y{t)ć_y, v(t) = \'x²(t)+y²{t)

(2.4)

a(t) • v(/) = *(/)c, ■* y(r)e_/t a{t) = \X²{t)*y²(t)

Składowe wektorów v(r), a{t) są odpowiednio równe

v,(/) * m*    v_y(t) = m

ajt) ^Ł x(t),    a_y{t) = y(t)

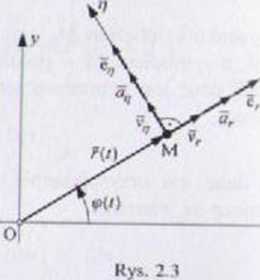
Układ współrzędnych biegunowych ni i rzuty wektorów v(r). a(t) w tym układzie przedstawiono na rys. 2.3. Współrzędnymi ruchu punktu są funkc • r(/). <p(r). Wektory r(/), v(t), a(t) oraz ich moduły wynoszą

r(r) = r(/)e_r(/),    |r(r)| - |r(f)|

v(/) = v (r)e_r(/) * v_n(/)e_n(r),    v(/) = y/v²(r) ♦ v²(r)

(2.5)

(2.6)

gdzie:

fl(0 - a,(i)e,(i) ♦    (0e„ (/), a(t) = y^fi) ♦ **(/)

v,(r) - r(t), v_n(0 « r(l)<p(f)

a_r{t) = r(f) - r(/)<jr (f),    «_n(r) = r(t)$(i) ♦ 2r(r)<p|f)

(2.7)

140

Kmcnalyfca. 1'mlsuwy tenretyem

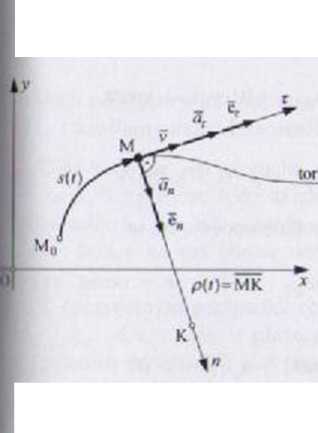
Układ współrzędnych naturalnych tri, wektor v(t) oraz rzuty wektora a(t) K tym układzie pokazano na rys. 2.4. Współrzędną ruchu jest funkcja s(f), ttyli przemieszczenie liczone wzdfuz krzywoliniowego toru punktu. Funkcja j(r) jest nazywana współrzędną torową. Ponadto, we wzorach występuje mień krzywizny p(t) tom ruchu punktu. Wektory v[t), a(t) oraz ich modu-p wynos/Jł

v(r) = v(r)e_t(r),    |v(r)| = |v(r)|

a{t) - a_x{t)e_r(t) ♦ aJt)e_H(t), aft) = _y'a_t^:(r) ♦ a²(t)

i²[t)

(2.8)

Izie:

(29)

P(f)

v(r) - i(l), a_x[t) = s(t)_y a_a(t)

A niektórych zadaniach korzysta się ze wzorów

(2.10)

V“(f )

<M'> = W). a_m(t) = ±22

P(0

lośli tor ruchu M jest opisany funkcją jawną y = /(*), to promień krzywizny tom

Rys. 14

PM -    * b'(*)f)'    (2.11)

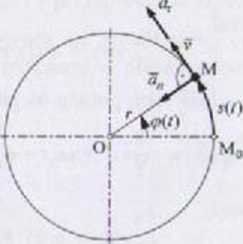
Rys. 2.5

Ruch punktu po okręgu pokazano na rys. 2.5. Prędkość i przyspieszenie punktu M najłatwiej obliczyć we współrzędnych naturalnych, ponieważ

p = r = consi    (2.12)

r.ie r jest promieniem okręgu. Prędkość v(f) oraz składowe przyspieszenia liczą się ze wzorów

v(f) - a>(f)r,    «_f(r) = e(f)r, ajt) * u²(t)r    (2.13)

141

h' rnutyka. Podstawy teoretyczne