mechanika82

Zadanie 2.5

Ruch punktu na płaszczyźnie jest opisany przez współrzędne x(f) = -2cos5r, y(t) = 3sin5r

Wyznaczyć funkcję y ■ f{x) opisującą tor ruchu punktu, położenie punktu w chw początkowej, wzory określające v(i), a[t) oraz v, o. p w położeniu A(0; 3 iii

Rozwiązanie Eliminacja zmiennej i:

y = 3sin5f => sin5/ = - =» sin²5r =

3    9

2

x = -2cos5r «=* cos5r = -- => cos²5/ = —

4

Tożsamość trygonometryczna: sin² 5/ + cos²5r = 1

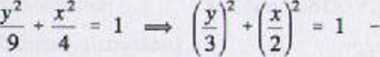
elipsa

Wykres toru ruchu punktu:

. i y

3lĄ_l

-2

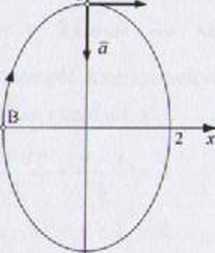
-3

r = 0:

x(0) = -2cos0 - -2*1 * -2 m y(0) = 3sin0 = 3-0 =0 W chwili r = 0 punkt jest w położeniu U

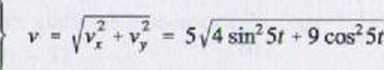
Prędkość i przyspieszenie: v_r - x{t) = 10 sin Sl

v_y = y(i) » 15 cosSl

164 KitHrmiilylui. 2.2.1. Kmcttitilyka punktu matcnalncga poins/.ii:jiv>!o tię \wdlu/ prostej

a_x = v,(f) ■ 50cos5/ ^ay * v_y(l) = -75 sin 5/

hniM A

K o =

-2 cos 5: = 0

=» cos5r = 0 =* 51 = — ==*■ t. =

2 ¹

s

* 10*1 = 10 m/s

10 m/s

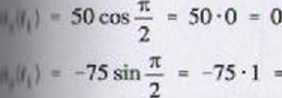
75 m/s²

v

2

a = fl_ve_yt a - 75 m/s²

= |*,| = 75 m/s²

—    1,33 m - promień krzywizny

/-•l unie 2.6

Hm i Krzywoliniowy punktu na płaszczyźnie jest opisany we współrzędnych Im. i nnowych

ml)    4 r²,    ip(r) = 2 sin 3/

Wyznaczyć funkcje v(r), a{t).

'jhr w iązanie

Ikm/ysUtmy ze wzorów (2.6) i (2.7).

I, - r = 8r

:ł_n = 4r-2-3cos3/ = 24r²cos3/

g, r - r<p^: = 8-4r²*(6cos3/)² = 8 - 144r²cos²3/

rq> ■ 2r«p - 4/^?*( 18sin3r) + 2• 8f-6cos3f = -72/²sin3t * 96rcos3/

¥H) '    +    = 8_v'r ♦ 9/⁴ cos² 3/

ui    y/a_r² + a²    8\/Tl - 18/²cos²3r)² + (12rcos3r - 9r²sin3r)²

H •' motyka 2 7 1. Kinematyka punktu materialnego ponii/ajaccgo się wzdłuż, prostej... 165