Mleko i śmietana (7)

Rozwiązanie za pomocą kwadratu Pearsona:

3.5

1.5-0.05 = 1.45

0.05

3.5-1.5 = 2.0

3.45 cz. mleka kotłowego

Wiedząc, że 10 000 kg mleka pełnego (3.5% tł.), którego udział w ogólnej; ilości mleka kotłowego (3.45 cz.) wynosi 1.45 części wagowych, można obliczyć liczbę kilogramów mleka odtłuszczonego z następującej proporcji:

1.45 cz, - 10 000 kg 2.0 cz. - X

_v 2.0 • 10 000

JŁ — --.    ■

1,45

13 793,1« 13 793 kg ml. odtł.

Całkowita ilość mleka kotłowego będzie zatem równa 23 793 kg.

Rozwiązanie za pomocą układu równań z dwiema niewiadomymi: Podstawą tej metody jest założenie, że liczba jednostek tłuszczowych (iloczyn zawartości tłuszczu i liczby kg lub dm³) przed i po normalizacji musi być taka sama. W celu rozwiązania powyższego zadania należy rozwiązać następujący układ równań z dwiema niewiadomymi:

(1.1)

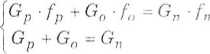
gdzie:

G_p - ilość mleka pełnego, kg lub dm³;

G_ó - ilość mleka odtłuszczonego, kg lub dm³;

G_n - ilość produktu normalizowanego, kg lub dm³; fp > |pJ| ~ odpowiednie zawartości tłuszczu, S§,

Podstawiając dane, otrzymuje się:

10 000 • 3.5 + G₍₎ -0.05 = G_n • 1.5 10 000 + G₀ = G„

35 000 + 0.05 G_n = 1,5 G G₀ p, G_n -10 000

[35 000 +	0.05 Gn - 500 = 1.5 G
\Gn - G„	-10 000
[i.45 a,,	= 34 500
Ho “ ^Gv	-10 000

a_n = 23 793.1 * 23 793 kg mleka o zaw. tf. 1.5%,

G_q = 13 793.1 *13 793 kg mleka odtł.

Korzystając z obu przedstawionych metod, można obliczyć każde zadanie normalizacyjne (zmniejszenie lub zwiększenie zawartości tłuszczu].

Podczas produkcji wyrobów mleczarskich zawartość tłuszczu można znormalizować w przepływie podczas wirowania mleka lub w zbiornikach normalizacyjnych (rozdz.9, t.l). W praktyce nie zawsze jest możliwe precyzyjne znormalizowanie zawartości tłuszczu w przepływie, dlatego często stosuje się normalizację dwuetapową. Pierwszy etap (normalizacja wstępna) polega na normalizacji zawartości tłuszczu przed homogenizacją i pasteryzacją. Drugi etap (normalizacja końcowa) jest przeprowadzany już po obróbce technologicznej, gdy stwierdzi się niezgodność rzeczywistej zawartości tłuszczu z żądaną. Do normalizacji końcowej należy używać mleka pasteryzowanego o takiej samej temperaturze jak mleko normalizowane.

Podczas produkcji jogurtu, koncentratów mlecznych, lodów lub serów należy; - oprócz normalizacji zawartości tłuszczu - także znormalizować zawartość suchej masy beztłuszczowej (smb) lub białka, co zostanie omówione w rozdziałach poświęconych poszczególnym wyrobom.

Homogenizacja

Emulsje typu olej w wodzie, takie jak mleko lub śmietanka, ulegają różnym zmianom fizycznym, które przyczyniają się do destabilizacji emulsji (rys.1.8), co objawia się powstawaniem warstwy śmietanki lub nawet wydzielaniem tłuszczu na powierzchni produktu gotowego. Aby zapobiec temu zjawisku, wykonuje się homogenizację polegającą na rozbiciu i dyspersji kuleczek tłuszczowych oraz ich skupisk do mniejszych rozmiarów.

W celu uzyskania pełnego efektu homogenizacji cała ilość tłuszczu musi występować w formie płynnej. Ważne jesttakże, aby temperatura homogenizacji była wyższa niż temperatura topnienia tłuszczu. Homogenizacja zimnego mleka, w którym tłuszcz jest w większości zestalony, jest nieefektywna. Homogenizacja stosowana w mleczarstwie polega na przepuszczeniu ogrzanego produktu pod wysokim ciśnieniem przez wąską szczelinę w homogenizatorze (rozdz.9, t.l). W efekcie homogenizacji uzyśkuje się kuleczki tłuszczowe o śr. 0.1-10 pm, przy czym zdecydowaną większość stanowią kuleczki o śr. poniżej* 2 pm. Na wiel-