82333

Część 1 12. METODA SIL LUKI 16

Dane zadanie rozwiążemy za pomocą bieguna sprężystego (siły nadliczbowe będą przyłożone na wspornikach o sztywności dążącej do nieskończoności). Luk posiada SSN=3. zatem układ podstawowy będzie mógł wyglądać następująco:

Część 1 12. METODA SIL LUKI 16

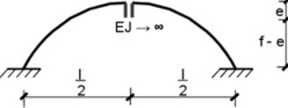
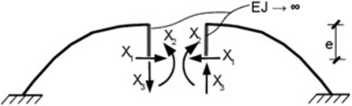
Układ równali kanonicznych zapewnia kinematyczną zgodność układu podstawowego. Wzajemne przemieszczenia odciętych przekroi muszą być równe zero:

(6_l=6_nX i+6_1:X_:+6 _lfX f+&,t=0

6_}=S_2I X,+6₂₂ X₂+ 6_2J X,+ &₂,=0    (12.34)

6 j= 6 _Jt X,+6 _J2 X ₂+6 _w X _s+A_{} r}= 0

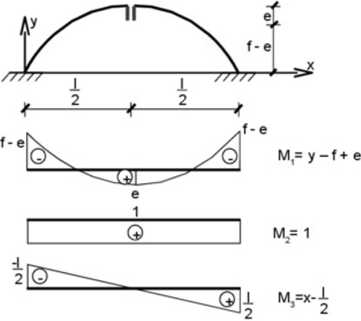
Mając dany układ podstawowy możemy narysować wykresy od akXi=l, X:=l i Xs-1 odnosząc je do Unii prostej (jest to odwzorow^ranie jedno-jednoznaczne w stosunku do wykresów odniesionych na kizywej hiku). Ponieważ łuk ma symetiyczną budowę a obciążenia dają symetiyczne lub antysymetryczne funkcje możemy określić, które w’artości przemieszczeń będą równe zeru:

AlmaMater

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdow^ka A.