82341

Część 1 10. METODA SIL RAMA 13

A,,= S

s

*,rS

s

4*-J

M,M°_P

EJ

ds

EJ

■ds

(10.16)

M.-K

EJ

■ds

Wykoizystując to we wzorze (10.13) zapiszemy:

^Tsr{-^ŁJj--d,=*;iX_r6,_l+X,S_l!+..+X.S_l.+A_lr)+

(10.17)

+Y~₂ (X, &j, + X, 6_r +... + X_m-6_im+A„)+

~Mt° Ał"

+r_m-(X_r6._l+X, S«+...+X.-6_m+A*)+S _v ' <k

Na mocy równań kanonicznych metody sil. wartości w nawiasach są równe zeru. Ostatecznie twierdzenie (10.11) zostało udowodnione.

m; m*

EJ

ds

(10.18)

10.2.2. Dowód drugiego twierdzenia redukcyjnego

W celu obliczenia dowolnego przemieszczenia w układzie statycznie niewyzmczalnym, wystarczy rozwiązać układ ten od obciążenia wirtualnego, zaś rzeczywisty stan obciążeń określić dla dowolnego układu podstawowego statycznie wyznaczalnego.

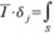
a/; m '

EJ

ds

(10.19)

Warto zaznaczyć, że dzięki twierdzenia redukcyjnemu w rozważanym układzie można pizeprowadzić bardzo dużo sprawdzeń kinematycznych, gdyż możemy pizyjąć wiele różny cli układów podstawowych. Reasumując, kontrole kinematyczną najlepiej przeprowadzać stosując inny układ podstawowy' niż wykorzystywany przy liczeniu niewiadomy cli. ponieważ efektem tego sprawdzenia byłoby tylko wykazanie poprawności równania kanonicznego.

Uwzględniając w obliczeniach pizemieszczeń jedynie wpływ momentów zginających udowodnimy twierdzenie redukcyjne w postaci:

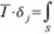
a/; at

EJ

ds=f

MpM”

EJ

■ds

AlmaMater

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A.. Wdowska A.