82346

Część 1 10. METODA SIL RAMA 21

E - 206,OJ GPa= 206,01 10*™

m

J-2140 10~*ni E J=4408,614 kN m^:

Ponieważ układ podstawowy przyjęto jak w poprzednim zadaniu możemy skorzystać z wykonanych wcześniej wykresów:

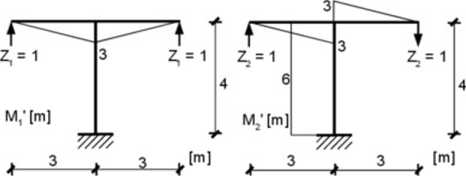
Rys. 10.24. Wykresy momentów zginających w układzie podstawowym pochodzące kolejno od: siły je dymkowej przyłożonej w miejsce niewiadomej Z, i siły jedynkowejprzyłożonej w miejsce niewiadomej Z,

i wcześniej obliczonych wartości niektórych współczynników:

/	(2— -3 3 ■—-3 \=1S —
EJ	\ ^2 3	/ EJ
62r
	EJ\2	3 2 3)
1	tft 1 ^3 i ii	6.6 )-9o’’L-
EJ	^IS + 2BJ^U	6 6 )-90 ej

a) Obciążenie teperaturą W układzie równali kanonicznych:

6 _n-Z,+6_1;-Z_;+An=0 6 ₂,■ Z,+6„• Z,+ A_2i = 0

brakuje jeszcze wyrazów wolnych. Obliczamy je według wzoru (10.22) pomijając wpływ/o.

- 40 + — 30 \=0,01S9 m

_ 1,2 10 * (3-" 0,20 \ 2

1,2 10 (3_1.₄₀ +LJ..30+6 4 10 \=0,0171

²¹    0,20 \ 2    2    I

Jeżeh cały układ równali pomnożymy przez EJ współczynniki ó,k będą liczbami, a wyrazy wolne będą miały wartość:

AlmaMater

Dobra D.. Jambrożek S.. Komosa M., Mikołajczak E.. Przybylska P.. Sysak A.. Wdowska A.