Scan145

14. ZJAWISKA TRANSPORTU

Miarą szybkości przepływu materii, ładunku lub pędu przez powierzchnię jednostkową w jednostce czasu jest strumień

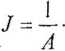
dj_

dt

gdzie A jest powierzchnią aj - przenoszoną wielkością.

Jest on najczęściej proporcjonalny do gradientu określonej własności układu (w procesach przebiegających blisko stanu równowagi).

Transport masy; pierwsze prawo Ficka:

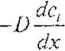
J_x

gd/.ic v oznacza współrzędną kierunku transportu, D - współczynnik dyfuzji danego składnika i, a rlcfi.y - gradient jego stężenia wzdłuż osi x.

I) jest wielkością charakterystyczną dla danego składnika w danym roztworze, zależną od tempera fury i, w przypadku roztworów rzeczywistych, od składu roztworu; typowe wartości D: I0’^ń do 10 ⁸ ctrr/s.

Rów nanie Smoluehowskicgo - Einsteina:

,v⁷- = 2D- At:,

gdzie a: “ jest średnim kwadratowym przesunięciom cząstki oci początku układu w czasie Al.

Lepkość dynamiczna (transport pędu); równanie Newtona:

F

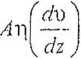
gdzie /' jest silą laicia. A - powierzchnią, (dulek) - gradientem prędkości przepływającej cieczy w kierunku a prostopadłym do jej mchu, a rą -jej lepkością dynamiczną (współczynnikiem lepkości dynomiczncj).

Równanie to jest słuszne tylko dla przepływów laminarnych i zawodzi często w przypadku płynów nie-newtonowskich, np. polimerów przy większych wartościach d\) kiz.

Silę tarcia można (eż obliczyć z zależności;

\

gdzie/jest współczynnikiem tarcia (stalą tarcia).

Równanie Stokesa - słuszne dla cząsteczek kulistych o promieniu r i przepływu ••

laminarnego    ■ /■

/ ćmy

Równanie Poiseuilłe’a: szybkość przepływu cieczy, x> (w cnr/sek) przez kapi-larę o promieniu r i długości / pod działaniem różnicy ciśnień AP,

% A Pr⁴

\) ~--

8r]l

Lepkość właściwa:

gdzie r\ jest lepkością roztworu substancji wielkocząsteczkowej, a % - jest lepkością rozpuszczalnika.

1l<j, = V(j),

gdzie <j> jest ułamkiem objętościowym substancji rozpuszczonej, a v - jej współczynnikiem asymetrii (odstępstwa od symetrii kulistej). Dla cząsteczek kulistych v =■• 2,5, dla elipsoid obrotowych v> 2,5.

Równanie Stokesa - Einsteina:

D = —‘—

6iu]r

gdzie t) jest lepkością dynamiczną ośrodka, a r - promieniem transportowanej cząsteczki (jonu).

14.1.Zadania

14.L W zjawiskach transportu układ osiąga stan stacjonarny, gdy gradient wielkości powodującej dane zjawisko transportu, dj!dx, (np. gradient temperatury przy przenoszeniu energii w postaci ciepła) osiąga wartość: a) stałą, b) maksymalną, c) zero.

14.2.    W większości metod stosowanych w pomiarach zjawiska transportu stan stacjonarny zostaje osiągnięty w bardzo krótkim czasie w porównaniu z czasem trwania pomiaru; a) tak, b) nie.

14.3.    Współczynnik przewodnictwa cieplnego, K , dla cieczy jest: a) 1 do 2, b) 3 do 4, c) 8 do 10, rzędów' wielkości mniejszy niż dla metali.

14.4.    Przyczyną dyfuzji danego składnika z danej fazy do fazy będącej

z nią w' równowadze jest.................

14.5A. Szybkość dyfuzji danego składnika w kierunku obszaru o niższym stężeniu tego składnika zależy od gradientu jego stężenia; a) liniowo, b) wykładniczo, c).............Zależność ta nosi nazwę prawa...............Współczynnik proporcjonalności w tym równaniu nosi nazwę współczynnika................