SDC10512

TaMfca 2-2

Rńimaała I wiarjr dn»ań harmonicznych przy (fumieniu lepkim

1. Og61ne równanie drgań tłumionych

d*z

dz

_jił-+e.-+*:»nO 12-11J ’ m^m m

dt

siła lepkiego oporu ruchu proporcjonalna do

prędkości. kN

inne oznaczenia -jak w tabl. 2-1

2. Równanie drgań własnych tłumionych j Rozwiązanie równania przy niewielkim tłumieniu, tj. (rys. 2-3)    | gdy c < X (najczęstszy przypadek)

d*z

~dt*

dz

—+a*r« 0    0-1211

d    i Oznaczenia:

z = ₍4e^-c,sin(A_l/+<p)

12-13]

e ---współczynnik oporu ruchu, s"^ł

2m

A i g? — patrz oznaczenia do wzoru [2-3]

2| = )/A²—c² » X— prędkość kątowa drgań własnych tłumionych

[2-15]

[2-16]

3. Równanie drgań wymuszonych tłu- Rozwiązanie równania [2-14] mionych wzbudzonych siłą harmonio-    _z _ ^sin(co/—ę>)

I Oznaczenia:

d*z _ dz    Pm .    A ** r* A₀ amplituda drgań wymuszonych, m

dt* di    m    I    ^we wzorze [2-6]

v_t— współczynnik dynamiczny (rys. 2-7)

1

V| =

przy czym:

2c

r“ ^T“

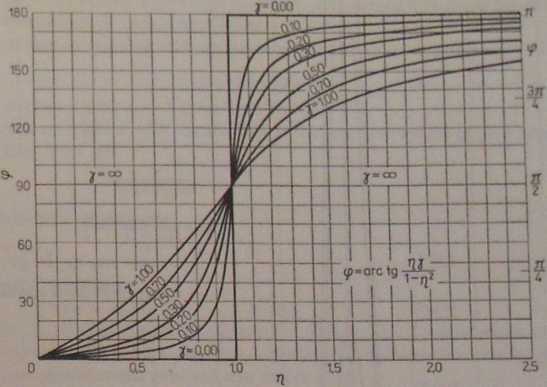
tp = arctg---_ — początkowa faza wymuszonych drgań

1 -y

V(i-rj*)²+yW

współczynnik tłumienia

(rys. 2-6)

”-7

[2-18]

T- |/ _1 +7**7*    [2-19]

r (R?+7?    ¹

4. Równanie drgań wymuszonych tłumionych wzbudzonych harmonicznym ruchem podłoża

• ■ io sińce/ d*z    I dz    dm\

dt*    \dt    dt I

0-17)

Rozwiązanie równania [2-17] z = 7Viosin(a>/—y)

Oznaczenia:

T— współczynnik przenoszenia drgań

— kąt fazy

y> = arctg

W

l-r)*+y²ti²

5. Siła przenoszona na podłoże

lub /»_r» i^,0 T8tn(oł/--v) [2-21]

JV~Ci-$-+Xz 0-20]

dt

We wzorach w tabl. 2-2 przyjęto założenie, że tłumienie drgań jest proporcjonalne do prędkości, co charakteryzuje opory ruchu spowodowane lepkością cieczy stosowanej w tłumikach drgań.

Tłumienie krytyczne, przy którym zanika ruch drgający, wyraża się zależnością

C_ikr = 2 /Km = 2mX.    [2-22]

Współczynnik tłumienia jest przyjmowany albo jako ułamek tłumienia krytycznego

C — CllClkr*

albo jako wartość dwukrotnie większa

y = 2C.    P-23]

Stopień tłumienia wyrażany jest przez dekrement logarytmiczny A, stanowiący naturalny logarytm stosunku amplitud w dwóch kolejnych okresach tłumionych drgań własnych (rys. 2-5)

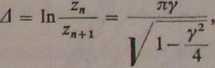
Rys. 2-6. Zmiana fazy drgań harmonicznych tłumionych

P-24j

skąd

y =

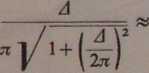
— (przy małym tłumieniu).

71

P-25]

Drgania tłumione nie są w ścisłym znaczeniu harmonicznymi ani nawet okresowymi. Jednakże uważamy je za harmoniczne stosując pojęcie umownego okresu drgań i umownej

75