skanuj0056 (Kopiowanie)

krzywą C = f (t) otrzymujemy¹:

CO    00

(8.8)

AUC - | Cdt = | Coe-^dt =

Ponieważ fikcyjne stężenie początkowe C₀ jest ilorazem dawki D i objętości dystrybucji Vd> otrzymuje się:

	^AUC - v%	(8.9)
skąd
	K • AUC -	(8.10)
Tak	obliczana objętość dystrybucji jest oznaczana	symbolem Vdpoie

lub Ffarea¹

Dzieląc objętość dystrybucji przez masę ciała (BW) otrzymuje się tzw. współczynnik dystrybucji lub względną objętość dystrybucji A'; czyli objętość dystrybucji na kilogram masy ciała (tab. 8.1)

^a'^1bW    ^^8,10

Sposób obliczania tych 3 parametrów ilustruje następujący przykład rachunkowy.

Przykład

Po dożylnym podaniu pewnej substancji leczniczej w dawce D = 50 mg znaleziono następujące stężenie w osoczu:

Czas W	0,25	0,5	1,0	2,0	4,0	5,0	7,0	10,0
Stężenie [mg/1]	6,0	3,5	1,6	1,1	0,45	0,32	0,13	0,041

Narysować przebieg tych zmian na papierze póllogarytmicznym, obliczyć stalą szybkości eliminacji, okres póltrwania, objętość dystrybucji i współczynnik dystrybucji.

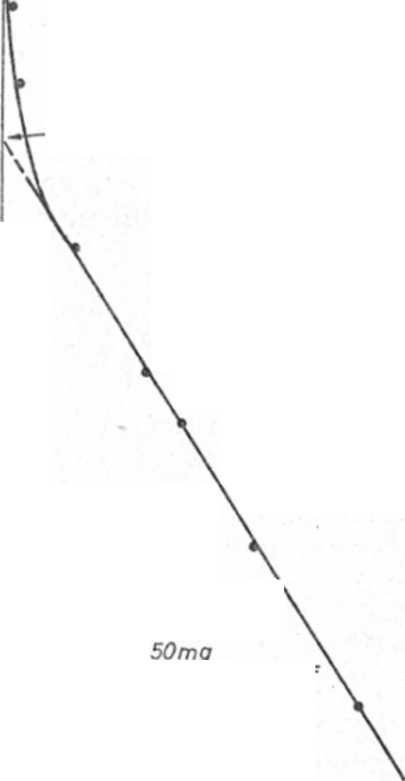
Rozwiązanie. Półlogarytmiczny wykres znalezionych stężeń przedstawiono na ryc. 8.2. Jak widać, poczynając od pierwszej godziny po wstrzyknięciu, stężenia substancji leczniczej w osoczu układają się w linii prostej.

Stałą szybkość eliminacji oblicza się korzystając z równania 8.1. Dla 2 dowolnych czasów t_i i t₂ stężenia substancji leczniczej w osoczu są równe C_Ł i C₂ i określone równaniami:

ln Cj ¹= ln Cj—Ki^ ln C₈ = ln C„—Kf_s

Odejmując je stronami, otrzymuje się po prostych przekształceniach:

K =

(8.12)

In C, —ln C₂

U-u

Dla t_x « 1 h i t_t = 10 h C, - 1,6 mg/1 i C₂ = 0,041 mg/1. Jednocześnie:

K =

ln 1,6—ln 0,041 _ 0,470+3,194

10 h — 1 h

9 h

= 0,407 h^_l

10P f- CC mg/U • (sAo/a log)

Znając stałą szybkości eliminacji oblicza się biologiczny okres półtrwa-nia, wychodząc z równania 8.6:

C₀=234 mg/l

Nachylenie --K

AUC= 5.75 mg- h/l

W -

01 ~

^V(j&>^,e=0.407h~^f ~S,75mgh/l = 2136 i

003'—¹—¹—¹—¹

J_i_i_i_L

7 2 3 4 5 6 7 6 9 10

K - lR¹⁶’t”0.041 __{0 AQ7t)}.i lOh-lh t_Q5=1-70h

y _    50 mg

^d 2.34 mg/l =2137 L

21.371    .

^A =-7Ó^~^:0-^30l/k9

tChJ

Ryc. 8.2. Półlogarytmiczny wykres zmian stężenia hipotetycznej substancji leczniczej podanej dożylnie w dawce D = 50 mg

to,5 =

0,693

0,693

K 0,407 h¹

\

= 1,702 h = 1,70 h

Ekstrapolowaną objętość dystrybucji obliczamy, wykorzystując równanie 8.7 i uwzględniając fakt, że początkowe stężenie substancji leczniczej C₀ = = 2,34 mg/1:

D _    50 mg

2,34 mg/1

= 21,371

Ponieważ chory ważył 70 kg, wobec tego współczynnik dystrybucji jest równy:

^A = w = °>^30I'^k«

Obliczając pole pod krzywą w granicach czasu od zera do nieskończoności otrzymujemy AUC—5,75 mg • h/l. Jednocześnie:

Kipcie =' _K.^_uc = 21,36 1

i ostatecznie:

^A = W ^{= 0}’^301/kg

8.3.2. Klirens

Inną metodę oceny szybkości eliminacji substancji leczniczej stanowa określenie jego klirensu. Pojęcie klirensu jest znane z fizjologii, a klirens kreatyniny Cl_cr jest powszechnie używanym wskaźnikiem czynności

Dożylne podawanie substancji leczniczych 111

1

W równaniach tych AUC jest skrótem ang. terminu Arca Undcr the Curve. Sposób obliczenia tego pola omówiono w rozdz. 10.

110 Zarys biofarmacji