str "

WPROWADZENIE DO GEOMETRII WYKREŚLNEJ

Geometria wykieślna jest nauką o metodach odwzorowań, które elementom podstawowym i tworom przestrzeni' przyporządkowują odpowiedniki - zwane obrazami -leżące na płaszczyźnie rysunku. Zadaniem poszczególnych metod jest podanie przepisów na takie odwzorowania, aby z obrazów elementów podstawowych i tworów przestrzeni można było odtworzyć ich kształt i położenie w przestrzeni. Odwzorowania takie pozwalają na wykreślnb rozwiązywanie zadań stereometrycznych, ponieważ określonym konstrukcjom w przestrzeni można przyporządkować ich odpowiedniki na płaszczyźnie rysunku.

Mamy kilka metod odwzorowań w geometrii wykreślnej, przy czym wszystkie posługują się rzutowaniem na płaszczyznę.

Omówimy dwa rodzaje rzutów: rzut środkowy i rzut równoległy.

Rzat środkowy

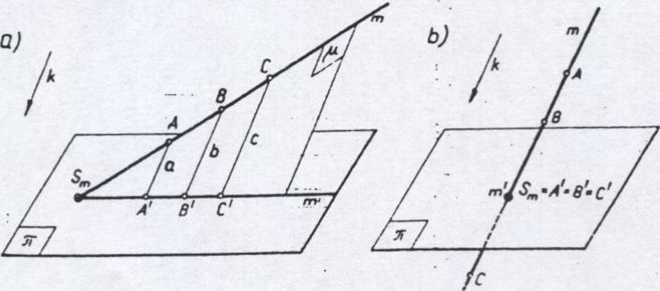
Przyjmijmy płaszczyznę x zwaną rzutnią, punkt O nie leżący na tej płaszczyźnie zwany Środkiem rzutowania oraz wiązkę prostych o wierzchołku O zwanych prostymi rzutującymi

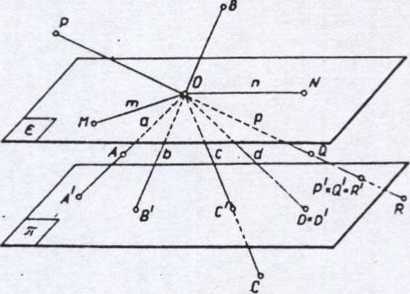
Rzutem środkowym punktu A na rzutnię n nazywamy punkt A', w którym prosta rzu-tuąca a, przechodząca przez punkty O i A. przebija rzutnię n.

Rzut równoległy

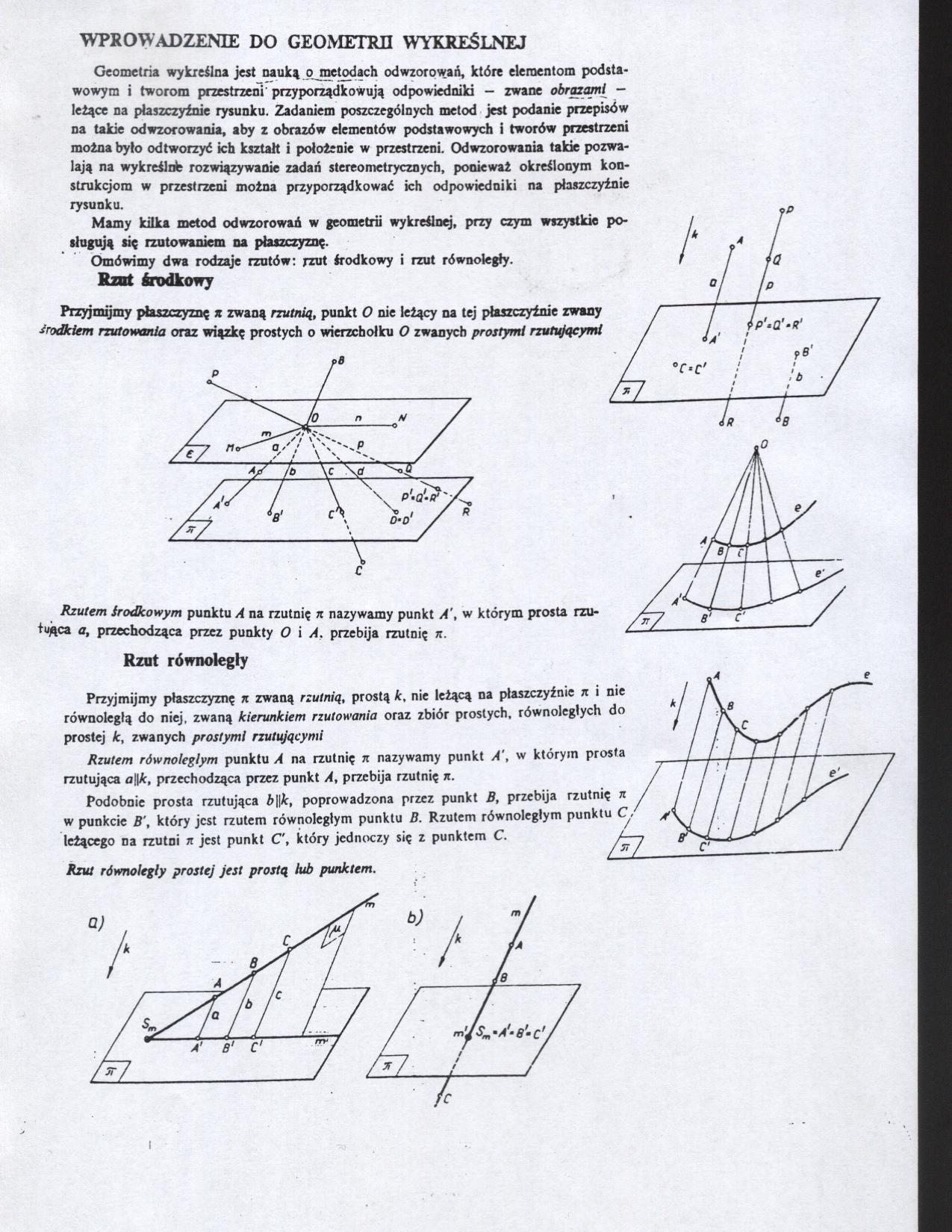
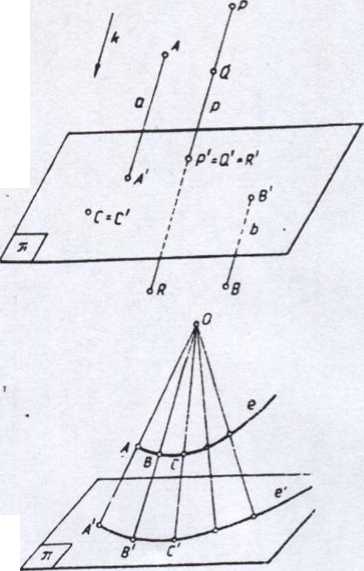
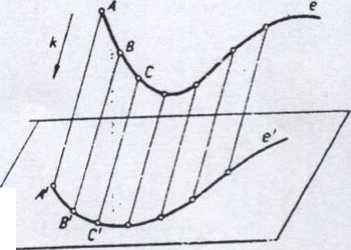
Przyjmijmy płaszczyznę n zwaną rzutnią, prostą k, nie leżącą na płaszczyźnie n i nie równoległą do niej, zwaną kierunkiem rzutowania oraz zbiór prostych, równoległych do prostej k, zwanych prostymi rzutującymi

Rzutem równoległym punktu A na rzutnię n nazywamy punkt A', w którym prosta rzutująca o||śr, przechodząca przez punkt A, przebija rzutnię n.

Podobnie prosta rzutująca h||it, poprowadzona przez punkt B, przebija rzutnię n w punkcie B', który jest rzutem równoległym punktu B. Rzutem równoległym punktu C\ leżącego na rzutni n jest punkt C', który jednoczy się z punktem C.

Rzut równoległy prostej jest prostą lub punktem.

i