szeregi liczbowe

Szeregi liczbowe

WZiE, sem.II, 2008-09 mgr K. Kujawska, SNM

Literatura:

[1]    Gewert M., Skoczylas Z., ANALIZA MATEMATYCZNA 2 Definicje, twierdzenia, wzory, Oficyna Wydawnicza GiS, Wrocław 2005

[2]    Gewert M., Skoczylas Z., ANALIZA MATEMATYCZNA 2 Przykłady i zadania, Oficyna Wydawnicza GiS, Wrocław 2006

[3]    Jankowska K., Jankowski T., ZADANIA Z MATEMATYKI WYŻSZEJ, Gdańsk 2004

Zad.l

Zad.2

[1] str.25, [2] 25-26.

Wykazać na podstawie definicji zbieżność następujących szeregów

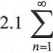
2

n² +n

2-2 £

1

(3w-2)(3/h-1)

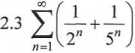
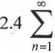
2” +3” 6”

Zad.3 Zad.4 Zad.5 Zad.6

[1] str.28, twierdzenie 2.1.10, ćwiczenie 2.1.11.

[1]    str.32, twierdzenie 2.2.10

[2]    str.33-34, przykład 2.4

Zbadać zbieżność podanych szeregów liczbowych korzystając z kryterium d’Alamberta:

oo 3 6.1 Y — IP	6.2 Y —- •	^00 „i 6.3 Y —-tJioo”	oo -n 6.4 Y—
6.5 f^3”^(n!)J H (2»)l	00 6.6 Y — h=l °	^00 ~,n 6.7 Y —	^00 1 6.8 Y II

[1]    str.33, twierdzenie 2.2.12

[2]    str.35, przykład 2.5

Zbadać zbieżność podanych szeregów liczbowych korzystając z kryterium Cauchy’ego:

Zad.7 Zad.8 Zad.9

₉₁ f(n + \)-5ⁿ

ZLd syn n=l ^

⁰⁰ _An

'•99”

3”

n=l

2».

4” -(n+2)"² n”²

100”

R=1

9.6 V —— ^?(n + 2)"

9._?M

9”V

9.4 Y- -

«=i

Zad. 10 Zad.l 1 Zad.12

[1]    str.30, twierdzenie 2.2.6

[2]    str.31, przykład 2.3

Zbadać zbieżność podanych szeregów liczbowych korzystając z kryterium porównawczego lub z warunku koniecznego zbieżności szeregów:

12 1 Y B	CO po y «	piY ^1	^00 i P1 V ^1
	“ 1000/7 +1 /!=1	" +	#2=1 +«
00 125 Y "	^00 1 V ^1	P7 Y ^1	^00 1 PU Y ^1
^f(^w + l)^2	V^w(^w + 1X^W + 2)	" £-(h + 1)(2* + 1)	' / 3 n=2\n —n

Zad. 13 Zad.14 Zad. 15

[1]    str.34-36, twierdzenie 2.3.1, definicja 2.3.4, twierdzenie 2.3.6, definicja 2.3.8.

[2]    str.39-41, przykład 2.8

Zbadać zbieżność podanych szeregów i określić rodzaj zbieżności:

15.1 ]T(-1)" n=l	n n^2+1	15.2 Y(-l)"-*	15.3 2>l)”«gJ ^1 B=I ' ^J	15.4 ^(-1)” 4 w=l ^11
oo 15.5 ]T(-1)" ««1	H*r]			15.8 Yf -^2" 1 iSWM
(-1)" 15.9 Y^IŁ “3» + l n=\		i5.io Y(-i)"4t?- ti » m	i5.il itil* n^2+4n + 3	15.12 Y K