UNTITL40

ROZSZYFROWAĆ RYXtK

Tabelu 3.1 Odchylenie standardowe dziennych zmian kursu (9.00-16.00i na ryj,, kach europejskich.

Kurs	1979-1994	1990-1994
CHF/USD	0.0070	0,0052
DEMUSD	0,0080	0,0056
JPY/USD	0,6000	0,3800
USD/GBP	0,0059	0.0063
USD/CAD	0,1119	0,1137
JPY.CHF	0,2900	0.3000
JPY/DEM	0.2400	0,2400
JPY/GBP	1,0700	0,7400
CHF/GBP	0,0081	0,0060
DEM/GBP	0,0091	0,0064
CHF/DEM	0,0012	0,0013
CAD/GBP	0,0072	0,0078

kursu obecny jest szum, a szum ten jest tym większy; im mniej wygładzone są dane, i dlatego kiedy wykres zbliża się lub przecina linię trendu, trzeba zawsze uwzględnić pewną przybliżoną wartość szumu. Pewne wyobrażenie o wielkości szumu daje tabela 3.1, w której podano odchylenia standardowe dziennych kursów otwarcia i zamknięcia dla szeregu walut notowanych w Europie w okresach 1979-1994 oraz 1990-1994 (patrz część czwarta). Odchylenia standardowe podane zostały dla dwóch nakładających się na siebie okresów 5- i 15-letnich, aby pokazać, że także one zmieniają się wraz z rozwojem iynku.

Wartości odchylenia standardowego wskazują na to, że nie powinno się panikować i uciekać ze statku, kiedy dochodzi do niewielkiego przecięcia linii trendu, a brak innych przesłanek odwrócenia trendu, ponieważ takie przecięcie może być wynikiem samego szumu. Powinno się o tym zawsze pamiętać, kiedy oblicza się prawdopodobieństwo P (patrz rozdział trzeci) danej linii trendu, w związku z czym małe przecięcie powinno być liczone jako pojedyncze odbicie, a nie dwa przecięcia.

3. Jak mówiliśmy wcześniej, linie trendu uzyskuje się prowadząc proste przez punkty odbicia, a punkty te wybiera się zazwyczaj na podstawie oceny wizualnej. Takie podejście, chociaż prawie zawsze poprawne, może przyczynić się do powstania dużych błędów, kiedy trzeba dokonać ekstrapolacji trendu na długi okres. Jeśli w takim przypadku zredukowanie błędów ekstrapolacji staje się konieczne, zazwyczaj wyznacza się najpierw wszystkie punkty, przez które zgodnie z oczekiwaniami ma przejść linia trendu, lub punkty' bliskie tym punktom. Następnie oblicza się i wykreśla linię najmniejszych kwadratów (patrz część dotycząca analizy regresji w rozdziale dziewiętnastym) z liniami kontrolnymi

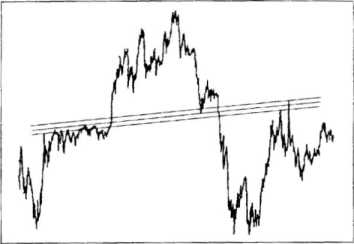
Diagram 3.3 Wykres kursu DEM/GBP ukazujący linię trendu uzyskaną metodą najmniejszych kwadratów, ze znajdującymi ąię poniżej i powyżej liniami kontrolnymi na poziomie 95 procent. Punkty użyte do obliczeń metodą najmniejszych kwadratów zostały wybrane drogą oceny wizualnej.

na poziomie 95 procent lub na innym poziomie ufności (diagram 3.3). Gdy liczba danych zwiększa się, może stać się konieczne dodanie nowych punktów lub pominięcie tych istniejących i ponowne obliczenie linii.

4.    Jak zauważono w rozdziale drugim, zakładamy istnienie trendu do momentu, w którym będziemy dysponowali wystarczającą ilością świadectw przemawiających na jego niekorzyść. Inaczej rzecz ujmując, jak mawiał pewien haitański przywódca, „skub kurę dopóty, dopóki nie zacznie gdakać".

5.    Linie trendu, w szczególności linie horyzontalne, mają największą siłę odbijającą lub odpierającą i zakłada się, że wpływ ten wzrasta w miarę jak wykres zbliża się do linii trendu. Oceniając bliskość kursu względem linii trendu należy' uwzględnić szum. Patrz rozdział trzeci.

6.    Mówiąc ogólnie, jeśli dwie lub więcej linii trendu znajduje się blisko siebie, wówczas wzmacniają się one wzajemnie, ale nie w sposób arytmetyczny. Jeśli na przykład mamy do czynienia z dwiema liniami określonymi prawdopodobieństwem sukcesu, czyli sile, równym P = 0,70 oraz 0,80, wówczas prawdopodobieństwo całkowite określające to, żc co najmniej jedna z linii się utrzyma, wynosi P, = 0,94. Patrz rozdział ósmy.

7.    Przecięcie ostro wznoszącej się linii trendu nie jest zwiastunem zmiany kierunku rynku, ponieważ wykres może równie dobrze