005 (54)

Zestaw 6

Zadanie 1. (4 pkt)

Punkt P(x, y) nazywamy punktem kratowym, jeśli obydwie jego współrzędne są liczbami całkowitymi. Uzasadnij, że jedynym punktem kratowym, którego współrzędne spełniają nierówność

\x² + 3y² < \ftixy,

jest punkt (0,0).

Zadanie 2. (5 pkt)

Wykaż, że równanie x⁴ — 4\/3x² +4 = 0 ma cztery różne pierwiastki. Oblicz sumę czwartych potęg tych pierwiastków.

Zadanie 3. (4 pkt)

Trzy pierwiastki wielomianu w(x) = xⁱ+px+q tworzą ciąg arytmetyczny o różnicy 4. Oblicz współczynniki p i q.

Zadanie 4. (4 pkt)

Naszkicuj wykres funkcji f(x) = |^y - 2|. Odczytaj z wykresu wartości parametru p, dla których równanie f(x) = p ma:

a)    dwa różne pierwiastki,

b)    dwa różne pierwiastki dodatnie.

Zadanie 5. (4 pkt)

Lewa strona równania 1+3 + 9+ ... + x = 1093 jest sumą kilku początkowych wyrazów ciągu geometrycznego. Oblicz y = 0,0(1) —

Zadanie 6. (5 pkt)

Wyznacz dziedzinę funkcji f(x) =    (^³ - 3x + 2).

Zadanie 7. (3 pkt)

Uzasadnij, że układ równań

f (x — 3)² + (y + 2)² = 5

\(a;-l)² + y² = l ma dokładnie dwa rozwiązania.

Zadanie 8. (6 pkt)

Rozwiąż równanie 11 — 4 sin (x — |) | = 1 dla x € (0; 2-k).

Zadanie 9. (3 pkt)

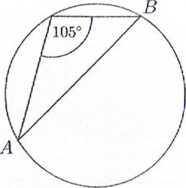
Promień okręgu (rysunek obok) jest równy 4\/2. Oblicz długość cięciwy AB.

Zadanie 10. (7 pkt)

W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa.

Zadanie 11. (5 pkt)

Rzucamy cztery razy symetryczną kostką sześcienną. Niech A oznacza zdarzenie polegające na tym, że przynajmniej raz wypadło 5 lub 6 oczek, a B - że w ostatnim rzucie wypadło co najwyżej 5 oczek. Które z tych zdarzeń jest bardziej prawdopodobne?

13. Zestawy maturalne 87