0063

64

I. Teoria granic

Pozostaje pokazać, że a' —a”. W tym celu niech n dąży w (1) do nieskończoności, najpierw przez wartości parzyste, a następnie przez nieparzyste. Otrzymujemy w granicy dwa związki

Odejmując je stronami rugujemy c:

(a' — a")(a' + a'' + 2)=0 .

Jak za chwilę ustalimy, przy c> —3 drugi nawias nie może się równać zeru, czyli musi być a' = a Rzeczywiście, w przeciwnym przypadku, podstawiając a" = —a' —2 w drugi ze związków (5) otrzymalibyśmy dla a' równanie kwadratowe

a'² + 2a' + (4+c)=0 ,

które właśnie przy O —3 nie ma pierwiastków rzeczywistych.

Poza tym przy c=—3 drugi nawias przyjmuje wartość 0 równocześnie z pierwszym, bo w tym przypadku a' = — 1 i a" = — 1.

Tak więc we wszystkich przypadkach a' = a”. Oznaczając wspólną wartość tych granic przez a, mamy na a wyrażenie (3), oczywiście ze znakiem minus przy pierwiastku, bo granica ujemnego ciągu {*„} nie może być dodatnia.

Podane przykłady prowadzą do następującej uwagi. Udowodnione twierdzenie jest typowym twierdzeniem o istnieniu: ustala się w nim fakt istnienia granicy, ale nie daje się żadnej metody obliczenia granicy. Niemniej omawiane twierdzenie ma ważne znaczenie. Z jednej strony w zagadnieniach teoretycznych często tylko istnienie granicy jest potrzebne, z drugiej strony, w wielu przypadkach możliwość poprzedniego przekonania się o istnieniu granicy jest dlatego ważna, że podaje sposób faktycznego obliczenia granicy. Tak np. w przykładach 1), 2), 3), 5), 6) właśnie wiedza o istnieniu granicy pozwoliła przez przejście do granicy w pewnych równościach ustalić dokładną wartość granicy.

W tym sensie jest szczególnie pouczający przykład 6) b). Chociaż przy c<— 3 wyrażenie (3) pozostaje sensowne, to nie wynika stąd w ogóle, że nadal określa ono granicę ciągu {x„}; przeciwnie, granica ta wtedy nie istnieje; łatwo np. sprawdzić, że przy c= —4 ciąg przybiera wartości:

-2, 0, -2, 0, -2, 0. ...

i nie ma granicy.

W przykładzie 4) nie mamy wzoru na granicę, ale wiedząc, że ta granica istnieje, możemy łatwo obliczyć ją z dowolnym stopniem dokładności, bowiem zawiera się ona pomiędzy ciągami {a„} i {/>„}, które dążą do granicy z obu stron.

W następnym ustępie zaznajomimy się z jeszcze jednym ważnym przykładem zastosowania twierdzenia o ciągu monotonicznym.

36. Liczba e. Wykorzystamy tu przejście do granicy dla określenia nowej nie spotykanej dotychczas przez nas liczby.

Rozważmy ciąg

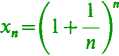
i spróbujmy zastosować do niego twierdzenie ustępu 34.

Ponieważ ze wzrostem wykładnika n podstawa potęgi tutaj maleje, więc bezpośrednio nie widać monotoniczności ciągu. Aby się o niej przekonać, przejdźmy do rozwinięcia na dwumian Newtona: