0091

92

II. Funkcje jednej zmiennej

lub

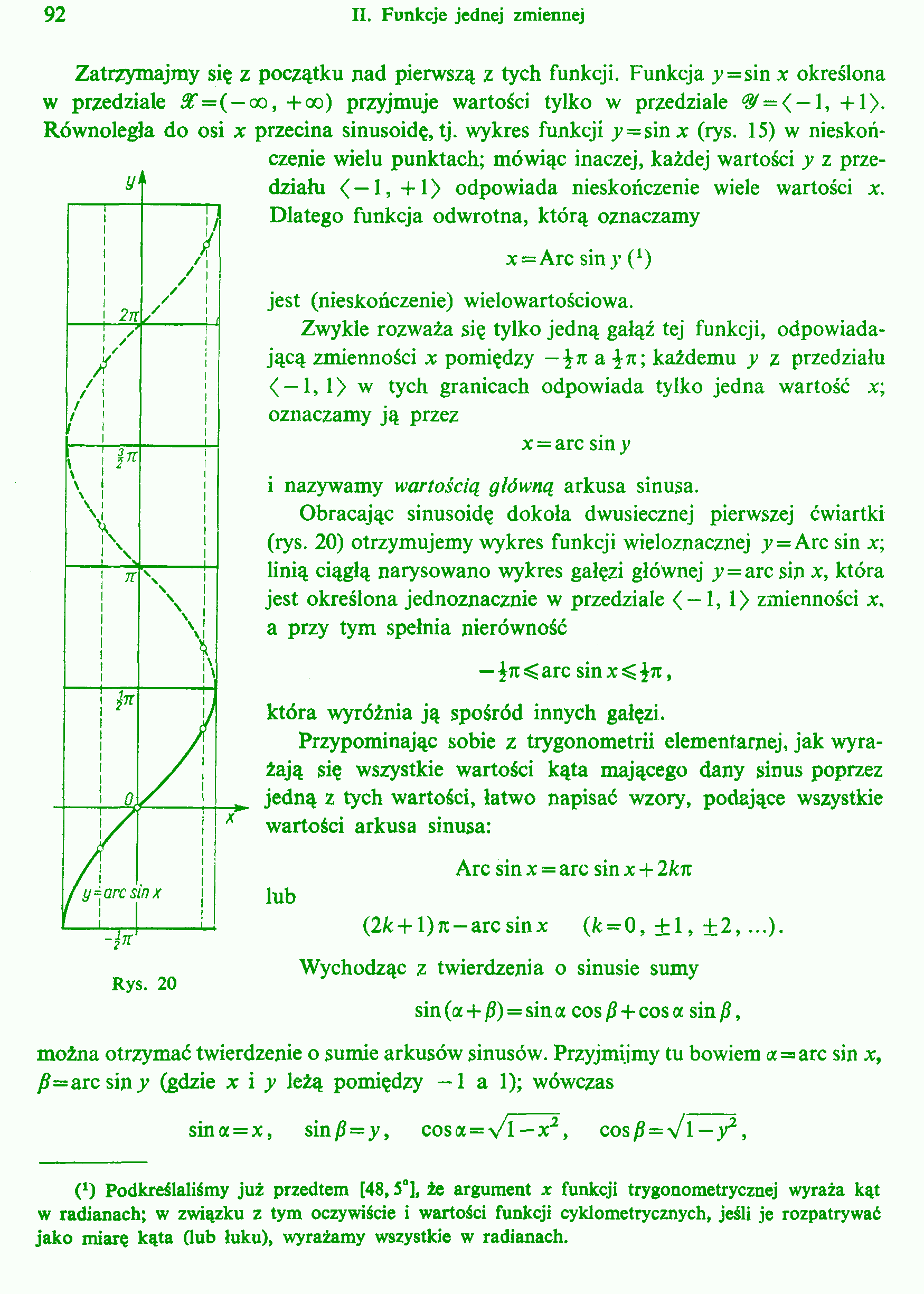
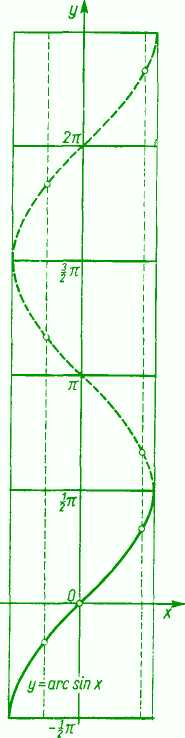
Rys. 20

Zatrzymajmy się z początku nad pierwszą z tych funkcji. Funkcja y=sin x określona w przedziale 3C=( —oo, +oo) przyjmuje wartości tylko w przedziale ^ = < — 1, +1). Równoległa do osi x przecina sinusoidę, tj. wykres funkcji y=sin;c (rys. 15) w nieskończenie wielu punktach; mówiąc inaczej, każdej wartości y z przedziału < — 1, +1) odpowiada nieskończenie wiele wartości x. Dlatego funkcja odwrotna, którą oznaczamy

x=Arc siny (¹)

jest (nieskończenie) wielowartościowa.

Zwykle rozważa się tylko jedną gałąź tej funkcji, odpowiadającą zmienności x pomiędzy — a %n; każdemu y z przedziału < —1, 1) w tych granicach odpowiada tylko jedna wartość x; oznaczamy ją przez

x = arc sin y

i nazywamy wartością główną arkusa sinusa.

Obracając sinusoidę dokoła dwusiecznej pierwszej ćwiartki (rys. 20) otrzymujemy wykres funkcji wieloznacznej y=Arc sin x; linią ciągłą narysowano wykres gałęzi głównej y=arc sin x, która jest określona jednoznacznie w przedziale < — 1, 1> zmienności x. a przy tym spełnia nierówność

—^7t<arc sinx^i7t,

która wyróżnia ją spośród innych gałęzi.

Przypominając sobie z trygonometrii elementarnej, jak wyrażają się wszystkie wartości kąta mającego dany sinus poprzez jedną z tych wartości, łatwo napisać wzory, podające wszystkie wartości arkusa sinusa:

Arc sin x = arc sin x + 2kn

(2fc + l)n-arcsinx (k = 0, ±1, ±2,...). Wychodząc z twierdzenia o sinusie sumy

sin (<¹+/?) = sin a cos/S+cosa sin/?,

można otrzymać twierdzenie o sumie arkusów sinusów. Przyjmijmy tu bowiem a=arc sin x, P—arc siny (gdzie x i y leżą pomiędzy —1 a 1); wówczas

sina = x, sin P=y, cosa = vl—:

cos

P=y/ l-J

1

Podkreślaliśmy już przedtem [48,5°], że argument x funkcji trygonometrycznej wyraża kąt w radianach; w związku z tym oczywiście i wartości funkcji cyklometrycznych, jeśli je rozpatrywać jako miarę kąta (lub luku), wyrażamy wszystkie w radianach.