0105

106

II. Funkcje jednej zmiennej

Wykres podano na rys. 23 (oczywiście niepełny — nie podobna wykreślić nieskończenie wielu

wahań!). Ponieważ przy zmianie znaku x również sin— zmienia znak, więc lewa połowa wykresu

x

jest symetryczna do prawej względem początku współrzędnych.

10) Jeżeli (dla x^0) rozważać funkcję x sin—, której wzór różni się czynnikiem x od tylko co 1 ^x

zbadanej funkcji sin—, to tym razem granica przy x->0 istnieje:

* 1

lim jc sin —=0 ,

*-.o    x

bo jest to od razu widoczne z nierówności

<l*i •

1

x sin — x

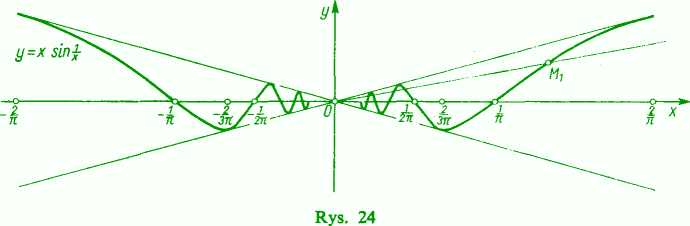
Gdy x dąży do 0, to rozważana funkcja ma również nieskończenie wiele wahań, ale ich amplituda (ze względu na czynnik x) maleje do zera, co zabezpiecza istnienie granicy.

Wykres funkcji

y=x sin — x

jest przedstawiony na rys. 24; wykres mieści się pomiędzy dwiema dwusiecznymi y=x oraz y=—x ćwiartek współrzędnych (’ )•

Uwaga. Mamy juz wiele granic

sin*    1

lim—=1 ,    lim (1 +*) =e , lim x sin—=0

i-0 X    I-O    I-O x

o tej samej osobliwości: ani jedna z rozważanych tu funkcji nie jest określona dla x=0. Nie przeszkadza to w omawianiu granicy tych funkcji, gdy jc-+0, bo zgodnie z dokładnym sensem podanej w ustępie 52 definicji wartość x=0 nie jest przy tym rozpatrywana.

Analogicznie, uwaga, że funkcja sin— nie ma sensu dla x=0, nie przeszkadza postawieniu py-

x

tania o granicę jej, gdy x-»0; tym razem jednak granica nie istnieje.

55. Rozszerzenie teorii granic. Powstaje naturalne zagadnienie rozszerzenia teorii granic ciągów, rozwiniętej w rozdziale I (§§ 1 i 2), na rozważany tu przypadek funkcji dowolnej. W tym celu można obrać dwie drogi:

(^l) Na rysunkach 23 i 24 dla jasności wzięto na osi x większą skalę, co powoduje pewne zniekształcenia rysunku.