015

15

1.2. Prawdopodobieństwo

geometrycznej definicji prawdopodobieństwa otrzymujemy

Pr (A) =

a¹ -Ar²

Przykład 1.2.6.

Z talii zawierającej 52 karty losujemy jedną kartę. Jakie jest prawdopodobieństwo, te tą kartą będzie pik lub figura (czyli as, król, dama lub walet) dowolnego koloru.

Rozwiązanie.

Niech

A, = {wylosowana karta jest pikiem},

A₂ = {wylosowana karta jest figurą}.

Szukamy prawdopodobieństwa zdarzenia A = A_x UA₂. Wynosi ono

Pr(A) =Pr(A₁)+Pr(A₂)-Pr(A,nA₂) = H ₊ A ₌ ^ «0.4808.

Przykład 1.2.7.

Na odcinku [0,1] umieszczamy losowo i niezależnie punkty x i y. Niech A będzie zdarzeniem polegający na tym, że x < y, natomiast B zdarzeniem polegającym na tym, że y < 0.5. Czy A i B są niezależne?

Rozwiązanie.

Zbiorem wszystkich możliwych wyników losowania jest CL = [0,1] x [0,1], Wtedy ^A = {(*>;y) e n : x < y}, B = {(x,y) eQ. :y< 0.5}.

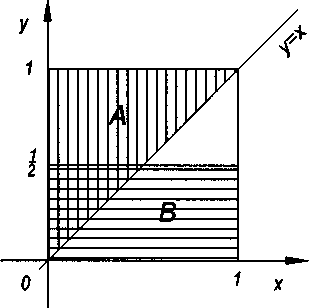
Rysunek 3:

Należy sprawdzić, czy zachodzi równość Pr(AnR) = Pr (A) Pr (fi). Ponieważ Pr(A) = Pr(fi) = 1/2 zaś Pr(AHB) = 1/8, (patrz rysunek 3), więc zdarzenia są zależne.