Matematyka 2 23

322 V. Elementy rachunku prawdopodobieństwa

3) Określamy pr-stwo 1*. tj. każdemu zdarzeniu A. przypora? kowujcmy pr-stwo P(A₍). Przyjmujemy, że zdarzeniu jednoelementowc >4 jednakowo prawdopodobne: P( (©,))=...= P( {(□*))= 1/8.

Przy obliczaniu pr-stw P(A,) korzystamy z własności P9 (I;

PIO):

P(A,) = P(0) = O.

P(A_25fe) = P(Q) = l

P(A₂)=...= P(A_v) = I/8,    P(A₁₀) = ...= P(A„) = 2/8 = l/4.

P(A,_g)-...= P(A_9ł)=3/8.    P(A_W )=...= P(A_ł6J)=4/8 = l/2,

P(A,_m) = ...= P(A,₁₉)=V8. P(A_22o) = ...= P(A₂₄₇) = 0/8 = 3/4 P(A_:4,)=,..= P(A_25s) = 7/8.

PRAWDOPODOBIEŃSTWO WARUNKOWE. Niech hę dana PP (il.ęĄ.P). Niech Be cĄ oraz P(B)>0. Dla dowolnego u rżenia A € cĄ liczbę P(A|B) (oznaczaną również symbolem P₈l określoną przy pomocy pr-stwa P równością

(2.1)

nazywa się pr-stwem warunkowym zdarzenia A przy warunku B

Funkcję zbioru P( |B) przyporządkowującą każdemu zdarzer Ae ^ liczbę P(A|B) zgodnie z (2.1), nazywa się pr-stwem warunkowym przy warunku B (w PI* (Q,<y^,P)).

Zauważmy, że pr-stwo P(A) dowolnego zdarzenia A może być traktowane jako pr-stwo warunkowe tego zdarzenia A przy warunku Q: [

(2.2)

p(A)^p.£P⁾«P(Ain).

Porównując (2.1) i (2.2) widzimy, że: pr-stwo warunkowe zdarzenia A przy warunku B zostało określone tak. jakby zdarzenie B pełniło rolę no-nttj PZE.

PRZYKŁAD 2.2. Wśród 10-osobowcj grupy studenckiej jest ośnuu studentów koleżeńskich, sześciu zdolnych; wiadomo poza tym. że wśród studentów zdolnych jest pięciu koleżeńskich. Doświadczenie polega na losowaniu studenta z tej grupy. Niech K będzie zdarzę* nieni polegającym na wylosowaniu studenta koleżeńskiego. Z - studenta

zdolnego. Obliczymy P(K|Z) - pr-stwo warunkowe wylosowania studen-_la koleżeńskiego, jeśli wiadomo, żc jest to student zdolny (por. rys 2.1).

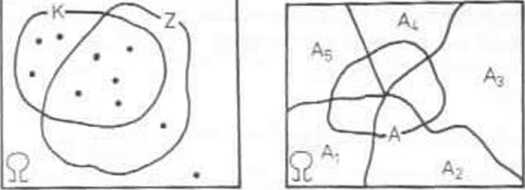
Rys 2.1.

Rys 2.2.

Mamy tu PP (0.^.1*), gdzie (2 = {zbiór dziesięciu studentów), cA - rodzina wszystkich podzbiorów PZE O, P - pr-stwo zgodne z definicją klasyczną. Korzystając z (2.1) otrzymujemy:

P(K |Z) =

P(KnZ) 5/10 5 P(Z) 6/10    6*

Pr-stwo wnrunkow-e P(K|Z) możemy, /godnie z wcześniejszym spostrzeżeniem, obliczyć tak jakby zdarzenie Z pełniło rolę nowej PZE i nie odwoływać się do pr-stwa P z PP (Q.^,P):

P( K|Z)=5/6

(jest sześciu studentów zdolnych. Z = 6, oraz wśród studentów zdolnych

jest pięciu koleżeńskich. KnZ=5 ).

Ten drugi sposób obliczania pr-stwa warunkowego wykorzystuje się przy obliczaniu pr-stwa koniunkcji zdarzeń.    ■

Prawdopodobieństwo koniunkcji. Bezpośrednio

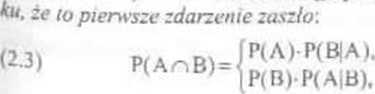
gdy P(A)>0 gdy P(B)>0 ’

^Zc wzoru (2 1) i przemienności koniunkcji zdarzeń wynika, że pr-stwo koniunkcji dwóch zdarzeń jest równe iloczy nowi pr-stwa dowolnego z ^l\ch zdarzeń i pr-stwa warunkowego pozostałego zdarzenia, przy warun-