Matematyka 2 41

340 V. Elementy rachunku prawdopodobieństwu

Punktami skokowymi x, ZL X są punkty nieciągłości dystrył anty, tj punkty -2. 0. 2, 3. Skoki p, = p(x,) = P(X = x_j) znajdujemy na podstawie własności F6 dystrybuanty Na przykład:

p j = p( 0) = P( X = 0) = F( 0*) - F(0) = 0.4 - 0.2 = 0,2 Analogicznie otrzymujemy: p, = p(0) = P( X = -2)=0.2.    p₃ = P(X = 2) = 0.4.    p₄ = P( X = 3) = 0,2. ]

Jak zwykle wyznaczoną funkcję pr-stwa zapisujemy w postaci tabeli:

X,	1 ^2	0	2	3
p,	1 0.2	0.2	0,4	0,2

PRZYKŁAD 3.8. Dana jest dystrybuanta F ZL X, (por

rys.3.8),

_r. . ]0 dla x<0 ^ * I l-e'³' dla x>0.

a)    Sprawdzimy, że X jest ZLC i wyznaczymy jej GP f.

b)    Obliczymy pr-stwo P(X>-j) korzystając tylko z dys‘ anty i podamy jego interpretację na wykresie dystrybuanty i GP f.

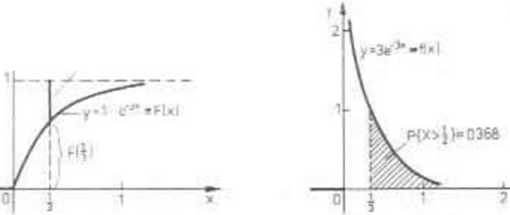
Rys 3.8

Rys 3.9

u) Dana dystrybuanta jest funkcją róźmczkowalną na całej osi 7 wyjątkiem punktu x = 0:

F'(x) = 0 dła x<0 oraz F'(x)=3e ^lx dla x>0.

Funkcja

0

dla x < 0

była dystrybuantą: a) ZLC. b) ZLS.

a) Funkcja F jako dystrybuanta ZLC jest ciągła (obustronnie) na całej osi, a więc również w punktach x = 0 i x = 1:

\->Ch

lim F(x)=F(l)o lim l = F(l)ol = a-l + boa=l.

jest postaci (3.11) i spełnia warunek unormowania (3.6). Zatem zgod

nie z twierdzeniem 3.4. X jest ZLC o GP f. (por. rys.3.9).

b) Suma pr-stw zdarzeń przeciwnych jest równa jedności, zatem

l>(X>i) = !-I’(Xsi)=l-P(X<|)=l-r(i) = c-' *0.368 ■

PRZYKŁAD 3.9. Dobierzemy tak stałe a i b aby funkcja F dana wzorem

lim F(x)»F(0)c* lim (ax + b)=F(0)oa-0+b = 0ob = 0,

Jeśli zatem F ma być dystrybuantą ZLC, to należy przyjąć a= 1, b = 0

b) Funkcja F jako dystrybuanta ZLS musi być przedziałami stała. Dlatego w tym przypadku należy przyjąć a = 0 Jest też zrozumiałe, że b może być dowolną liczbą z przedziału <0,1>. Zatem, jeśli a=0. b €<0.1 >. to dana funkcja F jest dystrybuantą ZLS.    ■

ZADANIA DO ROZWIĄZANIA

1. Dana jest funkcja pr-stwa ZL X:

X,	I ^1	3	5	7	10
Pl	1 OJ	0,1	c	0,2	0,3

Wyznaczyć: a) stałą c. b) wykres i histogram funkcji pr-stwa,

c) dystrybuantę i jej wykres, d) pr-stwa: p, = P(X = 3) ,p_; = P( X = 2). p, = P(X<7)_t p₄ = P(X<IO). p₅ = P(X>3), p₆ = P(3<X<7), p₇ = P(-5<X<7). p_s = P(|X-5|<3), p_f=P(|X-3j>l) dwiema metodami korzystając: 1) tylko z danej funkcji pr-stwa oraz 2) z N*7zna-czonej dystrybuanty; znalezione pr-stwa p, zaznaczyć nu rysunku z wykresem dystrybuanty