Matematyka 2 43

342 V. Elementy rachunku prawdopodobieństwu

2.

Dana jest dystrybuanta ZLS X:

X | (-00,-3 >	*(-3,0>	(0,4 >	(4,9 >	(9,I5>	(!5.oo)
F(x) | 0	0.2	0.4	0.7	0,8	1

Wyznaczyć funkcją pr-stwa ZL X.

3.

4.

5.

a)    Wyrazić za pomocą dystrybuanty następujące pr-stwa: p, = P(X£b), p> = P(X^b), p₃ = P(u<X^b). p₄ = P(a<X<b), p_} = P(a < X < b), gdy X jest ZLS;

b)    uprościć odpowiedzi do zadania a), gdy X jest ZLC;

c)    korzystając z a) obliczyć pr-stwa: p, = P(X<9),p₂ = P(4<X£ 15), p_} = P(4 < X < 15), gdzie X jest ZL z zadania 2.

Niech w- warunkach przykładu 3.1 Y oznacza liczbą maszyn, które w ciągu godziny nie wymagały interwencji pracownika. Wyznaczyć funkcją pr-stwa ZL Y. Porównać otrzymany wynik z funkcją pr-stwa ZL X wyznaczoną w przykładzie 3.3. Uzupełnić zdanie: "dwie różne ZLS mogą mieć jednakowe

Ze zbioru siedmiu odcinków, wśród których trzy są długości 3 cm każdy i cztery mają długość 5 cm każdy, losujemy trzy odcinki. Każdemu trójkątowi zbudowanemu z tych odcinków przyporządkujemy obwód. Wyznaczyć: a) funkcją pr-stwa, b) dystrybuantą tak określonej ZL.

6.    Spośród wierzchołków sześciokąta foremnego o boku długości l cm wybrano losowo trzy różne. Każdemu trójkątowi o wierzchołkach w wylosowanych punktach przyporządkowujemy jego pole. Wyznaczyć: a) funkcją pr-stwa, b) dystrybuantą tak określonej ZL.

7.    Danajesi funkcja f: r(*)={*^(Hx_l|) ^

a) Wyznaczyć stałą a tak. aby funkcja ta stała się GP pewnej ZL X; naszkicować jej wykres.

b)    Wyznaczyć dystrybuantą ZL X i naszkicować jej wykres.

c)    Korzystając bezpośrednio z GP i wyznaczonej dystrybuanty obliczyć pr-stwa: p, = P(X<l), p, = P(|X-1|<0,5), p, = P(X-2X^: >0),

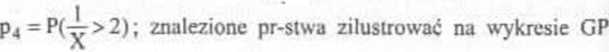
wykresie dystrybuanty.

Dana jest funkcja f: f(x) =

~coS"źj-x dla 0<x<jt O    dla x £ O v x > n.

a)    Sprawdzić, żejest to GP pewnej ZL X, naszkicować jej wykres.

b)    Wyznaczyć dystrybuanty ZL X i naszkicować jej wykres.

c)    Obliczyć pr-stwa: p, = P(X<n/2), p₂ = P(X>n/3),

p, = P(ti/3< X <tt/2) i zaznaczyć je na wykresie GP i dystrybuanty.

9. Dana jest GP f ZLC X. Wyznaczyć jej dystrybuanty F (wzór i wykres) oraz obliczyć pr-stwa p_k .jeśli:

a)    f(x) =

b)    f(x) =

c)    f(x)=

d)    f(x) — c) f(x) = 0 f(x) = <

g)    f(x)=

h)    f(x) =

1*73	dla — 1 < x < 2	P,=P(X<1).
0	dla x<-l v	x>2; p3 = P(0<X< 1);
J3(x-	l)^2/2 dla 0<	x<V p,=P(|X-l|<0,5),
10	dla x£	0 V x2>2; p2 = P(4X^2-8X + 3
*74	«N V X V O J2	p, = P(|X-1|> 0.5),
0	dla x<0v x^2;p2sP(p^>0);
r	dla x>l, dla x<l;	Pi = P(X<3). p3 = P(X>2);
{V,^3	dla x> 1,	Pi =P(4-X^3 >0),
0	dla x < 1;	p3 = P(X^J>4X);
l/2*/x dla 1 <x<4		p,=P(|X-3|<l).
0	dla x ^ v	x>4; p2 = P(X^3 -4X <0);
J2e‘^2x dla x>0		Pl = P(X> l/X),
1°	dla x<0.	P2 = P(X—i > l/(X—1)):
lnx	dla l<x<e.	P| = P(X<VÓ,
1°	dla x$l v x2	:c; p2 = P(X>e/X);
Hx|	dla |x|<l.	P, — P(|X|< 0.5),
	dla |x|>l;	Pj = P(2X^J-5X+2 <0);