Matematyka 2 97

396 V Elementy rachunku prawdopodobieństwu

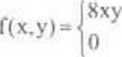
2. Dana jest GP WL(X.Y):

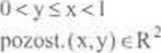
a) Obliczyć pr-slwa:

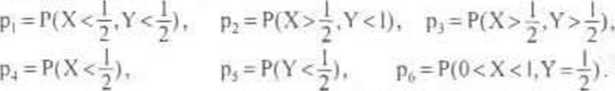
b)    Wyznaczyć brzegowe gęstości pr-stwa i brzegowe dysirybuanty.

c)    Obliczyć wartość oczekiwana i wariancje ZL X i ZL Y

d)    Rozstrzygnąć, czy ZL X, Y są niezależne.

c) Wyznaczyć warunkowe (iP. warunkowe dystrybuanty. warunkowe wartości oczekiwane

0 Wyznaczyć kowariancję i współczynnik korelacji ZL X, Y. g) Wyznaczyć linie regresji pierwszego rodzaju, hl Wyznaczyć obie prosie regresji drugiego rodzaju.

3 Wyznaczyć gęstość pr-stwa wektora losowego (X\Y) mając dane: brzegową GP f_x i warunkowądyslrybuantę F_Y(|x)

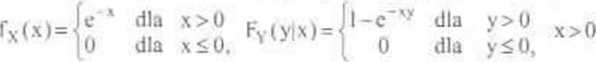
4 Rozstrzygnąć, czy ZL X i Y są: 11 niezależne. 2) mcskorelowane. gdy wektor losowy ciągh (X.Y) mu:

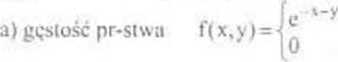
dla x>0 a y>0 dla x < 0 v y<0.

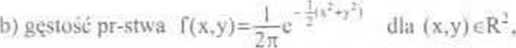
c) rozkład jednostajny w kwadracie D o wierzchołkach (-1,0). (0.-1), (1.0). (0,1), ij rozkład zadany gęstością pr-.st\va (2 jest polem danego kwadratu D):

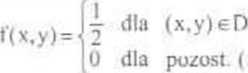
x.y).

d) rozkład jednostajny w kole x^: 4-y^:<r³ 5 Oszacować z góry cov(X,Y), jeśli VorX=25. VarY = 4.

h Wykazać. ze \ ar( XY) = VarX- VarY wtedy i tylko wtedy, gdy EX=0 i EY = 0.

7. Oblicz>x Var(XY) wiedząc, że ZL X. Y są niezależne oraz EX = -2, FY = 3, VarX=3, VarY=l.

8 Obliczyć Var(3X-4Y),jeśli VarX = l, VarY = 2, cov(X.Y)=|.

9. a) Obliczyć cov(U,V), jeśli: U = 2X-3, V=-3X+2. VarX = 2.

b)    Obliczyć p_x.2x+i» Px.-:x.m Px-j.-jx*2*

c)    Dokonujemy 5 doświadczeń Bernoulliego z pr-stwem p sukcesu w pojedynczym doświadczeniu. Niech X oznacza liczbą sukcesów w tych pięciu doświadczeniach, Y • liczbę porażek. Obliczyć: cov(X.Y), p^_Y.

10.

at ZL X przyjmuje wartości -3, 0. 3 odpowiednio z pr-stwami: 0.25, 0,5, 0.25 Niech Y = X* Wykazać, że ZL X,Y są nicskorelowanc (mimo, że są funkcyjnie zależne), b) ZL X ma gęstość pr-stwa postaci:

^cosx

f(xL

dla —zę < x <— *

dla pozost x

Niech Y = X-. Sprawdzić, żc ZL X. Y są nieskorclowane.

! I a) Jaki punkt jest punktem wspólnym obu prostych regresji drugiego rodzaju?

h) Kiedy proste regresji drugiego rodzaju pokrywają się?

c)    Kiedy proste regresji drugiego rodzaju są prostopadle do osi układu?

d)    Prosta y 2x-3 jest linią regresji pierwszego rodzaju ZL Y|X. Napisać równanie prostej regresji drugiego rodzaju ZL Y X. Wynik uzasadnić.

Odpowiedzi

I ai p, —0.25, p_: -U.05. pj = 0.-40 p,-0,65. p=-0,75, p,. -0.25, p = U.35.

p, - 0.15. p.-O

b)	X,	II ~^10	0	10		0	10
	P,	I 0.25	0.40	0.35	Pi	1 °-^45	0.55