Matematyka 2 53

352 V. Elementy rachunku prawdopodobieństwu

352 V. Elementy rachunku prawdopodobieństwu

Zatem: jeśli GP f ZL X będziemy interpretować jako gęstość masy jedr wej rozmieszczonej w sposób ciągły wzdłuż osi 0x, to wartość oczekiwana HX Jtjf współrzędną środka lej masy.

PRZYKŁAD 4.5.. Wyznaczymy wartość oczekiwaną E.X ZLC X o rozkładzie wykładniczym z parametrem /., tj. o rozkł

zadanym GP postaci:

f(x)=

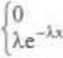
dla x£0 dla x>0,

X>0.

GP f jest tu skoncentrowana na dodatniej półosi, zatem zbieżn bezwzględna całki po prawej stronie (4.2) jest równoważna zwyk zbieżności. Kolejno otrzymujemy:

Bardzo często zachodzi potrzeba wyznaczenia wartości oczekiwanej ZL Y = g(X) będącej daną funkcją g ZL X. gdy dany jest rozkład pr-stwa ZL X. Wydawałoby się, że jedyna droga to: wyznaczenie najpierw funkcji pr-stwa ZL Y (gdy jest to ZLS) albo GP ZL Y (gdy jest to ZLC) i następnie zastosowanie wzorów (4.1) lub (4.2). Okazuje się, że nic jest to konieczne. Dowodzi się bowiem, ze:

Wartość oczekiwana Eg(X) wyraża się bezpośrednio przez funkcję pr-stwa p( ) lub GP f ZL X następującymi wzorami:

(4.3)

(4.4)

Eg(X)=£g(x,)p(x,).

I,€W

OC

Eg(X)= Jg(x)f(x)dx pod warunkiem, że szereg i całka po prawych stronach tych wzorów są bezwzględnie zbieżne.

W jednej z omawianych niżej własności wartości oczekiwanej mówi się o niezależnych zmiennych losowych. Sformułujemy teraz to pojęcie. Wiąże się ściśle ono z poznaną już niezależnością zdarzeń. Bardziej szczegółowo o niezależności ZL będziemy mówić w paragrafie 7.

Mówimy, że ZL X i Y są niezależne, gdy dla dowolnych x,y gR /darzenia {w: X(co) < x} i {co: Y(to)<y} są niezależne, czyli (4.5) P(X<x,Y<y) = P(X<x) P(Y<y) dla dowolnych x,y gR .

Analogicznie określa się niezależność dowolnej skończonej liczby zmiennych losowych X|_tX₂,.-.,X_B. Natomiast o zmiennych losowych nieskończonego ciągu Xj,X₂....,X_n,... powiemy, że są niezależne, gdy dla każdego ustalonego n niezależne sąZL X|,X₂,...,X_n

Wartość oczekiwana ZL jest sumą lub całką Można wobec tego oczekiwać, że ma ona własności podobne jak suma i całka. Zobaczymy, że istotnie tak jest.

TWIERDZENIE 4.1. Wartość oczekiwana ZL ma następujące własności (X*Y - ZL dowolnego typu, a, b, c - dowolne stałe): El, E2. F.3. E4. E5-

El. Jeśli P(X = c) = I, to EX~c; jeśli P(X>0)=1, to EX>0; jeśli P(aśX<b) = l, to a<EXSb; jeśli P(X£Y) = l, to EX<EY; w szczególności EX<E|XJ.

E2. Jeśli istnieje EX, to istnieją E(aX), E(X^-b), E(aX+b)

oraz

E(aX) = aEX, E(X + b) =* EX+ b. E(aX+ b) = aEX + b.

W szczególności: dla każdej ZL X, dla której istnieje EX. mamy:

E(X-EX) = 0.

E3. Jeśli istnieją BX i EY, to istnieje E(X±Y) oraz E(X± Y) = EX±EY.

E4. Jeśli ZL X i Y są niezależne oraz istnieją EX i EY. to istnieje E(XY) oraz

E(XY) = EXEY

E5. Jeśli istnieje EX oraz krzywa gęstości (dla ZLC) lub histogram funkcji pr-stwa (dla ZLS) są symetryczne względem prostej x = x₀ (rozkład pr-stwa ZL X jest symetryczny względem punktu x = x₀). to P.X=x₀.