Matematyka 2 55

354 V. Elementy rachunku prawdopodobieństwa

D o w 6 d. Ograniczymy się do dowodu pierwszej własności FI, trzeciej własności E2 oraz własności E5. Na mocy definicji EX, (wzór (4.1)), mamy;

EX=2>,p(x,)=e P(X = c)=c l=c

«,kW

Przechodzimy do dowodu trzeciej własności E2. Gdy X jest ZLS, to zgodnie z równością (4.3), w której przyjmujemy g(X) = aX + b i warunkiem unormowania (3.2), mamy:

E(aX + b) = £(ax +b)p(x₍) = a £xiP(x,) + b£p(x.) = aEX + b.

ft.cW    X.€W    »,*w

Podobnie, gdy X jest ZLC o GP f, to na mocy równości (4.4) i warunku unormowania (3.6). mamy:

co    ao    06

E(aX + b) = J(ax + b)f(x)dx=a Jxf(x)dx + b Jf(x)dx = aEX + b.

Ważna rownośc E(X-EX) = 0 wynika z udowodnionej wyżej równości, jeśłi przyjąć w tej równości a = I i b = -EX.

Dowód własności E5 przeprowadzimy tylko dla ZLC. Z założenia EX istnieje, więc

ac    *«    «

EX= Jxf(x)dx= Jxf(x)dx+ fxf(x)dx.

-o¹    -co    Xn

Wykonując w całkach po prawej stronie odpowiednio podstawień' x=x₀—t, x = x₀ +1, otrzymujemy;

+06    -Kr

EX = J(x₀“t)f(x₀-t)dt+ J(x₀ -ł- l)f(X₀ -t-t)dt o    o

Z założenia GP f jest symetryczna względem prostej x = x₀, więc

* 1

f(Xo-t)= f(.x₀-M) dla każdego t oraz [f(u)du = -. zatem

EX = 2x₀ Jf(x_n+t)dt=j*^~^U = 2x₀ Jf(u)du = 2x_n-i = x₀. Ą

KWANTYLE. Poznamy leraz charakterystyką liczbową ZL przydatną w następnym rozdziale Ograniczymy się do ZLC. Niech zatem _P€(0,l).

Kwanty lent rzędu p ZLC X o dystrybuancic F i GP f nazywamy liczbę x_p. spełniającą którykolwiek z następujących równoważnych

warunków:

(4.6)    F(x_p)=p, P(X<x_p)=p, Jf(x)dx=p.

KwantyI rzędu p = 0,5 nazywa się medianą

W interpretacji geometrycznej kwantyl x_p ZLC X ó dystrybu-aneic F i GP f jest:

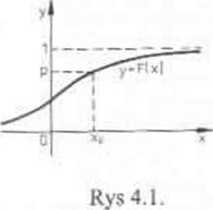
1)    odciętą x_p punktu przecięcia prostej o równaniu y = p z wykresem dystrybuanty y=F(x). czyli pierwiastkiem równania F(x) = p, (por. rys 4.1),

2)    odciętą x_p takiego punktu na osi 0x, że pole pod krzywą GP y=f(x) nad przedziałem (-oo,x_p) jest równe p. (por. rys 4.2).

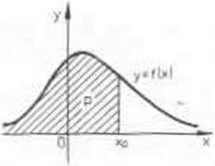
Rys 4.2.

PRZYKŁAD 4.6. Wyznaczymy kwantyl x₀₉ ZLC X z przykładu 4.5 dla ). = 2.

W znany sposób wyznaczamy najpierw dystrybuantę F ZL X:

_D .    |0    dla x£0

^F(x)“|l-c'^u dla x>0.

Zrozumiałe, źe x_ e(O.oo) Zatem rozwiązując równanie

F(x) = p, czyli 1-e    = p, otrzymujemy x =-—łn(l-p).