Matematyka 2 35

334 V. Elementy rachunku prawdopodobieństw

y

y

x, O

X, X

O

X

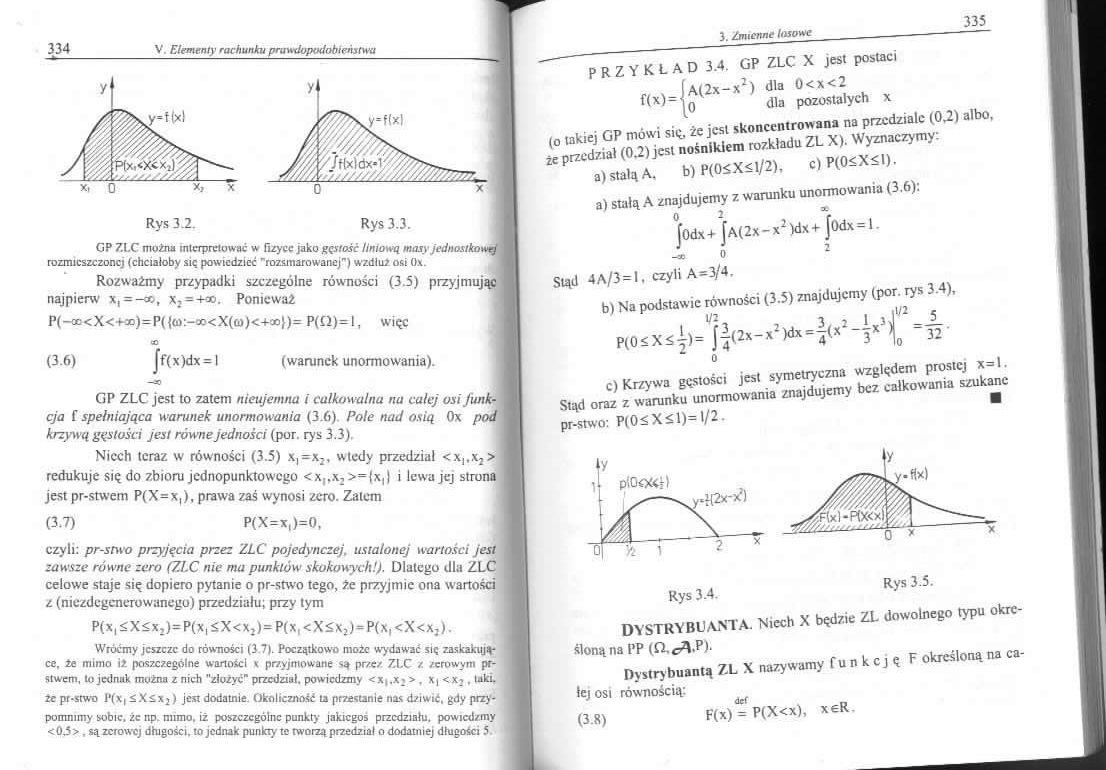
Rys 3.2.

Rys 3.3.

GP 7.LC można interpretować w fizyce jako gęstość liniową masy jednostko rozmieszczonej (chciałoby się powiedzieć "nasmarowanej") wzdłuż osi 0x.

Rozważmy przypadki szczególne równości (3.5) przyjmując najpierw x, = -<*», x_; = -ko. Ponieważ

P(-oc<X<+oo)=P({(o:-:»<X(a))<-t-ao})= P(Q)=I, więc

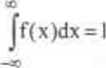
(warunek unormowania).

GP ZLC jest to zatem nieujemna i całkowalna na całej osi Junk

cja f spełniająca warunek unormowania (3.6) Pole nad osią 0x pod krzywą gęstości jest równe jedności (por. rys 3.3).

Niech teraz w równości (3.5) x,=x_:, wtedy przedział <x,,x₂> redukuje się do zbioru jednopunktowego <x,.x_: >={x,| i lewa jej strona jest pr-stwem P(X=x,)_t prawa zaś wynosi zero. Zatem

(3.7)

P(X=x,)=0,

czyli; pr-srwo przyjęcia przez ZLC pojedynczej, ustalonej wartości jest

zawsze równe zero (7.1.C nie ma punktów skokowych!). Dlatego dla ZLC celowe staje się dopiero pytanie o pr-stwo tego, że przyjmie ona wartości z (niezdcgcncrowancgo) przedziału; przy tym

P(x,<X<x₂)=P(X|<X<x₂)=P(x,<X<x₂)=P(x_l<X<Xj).

Wróćmy jeszcze do równości (3 7). Początkowo może wydawać się zaskakujące, że mimo iż poszczególne wartości v przyjmowane są prze/. ZLC / zerowym pr-stwem, to jednak można z nich "złozyć" przedział, powiedzmy <x_t.x> > . X| <x₂. taki. ze pr-stwo P(X| ^Xsx₂) jest dodatnie Okoliczność ta przestanie nas dziwić, gdy przypomnimy sobie, żc np mimo. iż poszczególne punkty jakiegoś przedziału, powiedzmy <03> . są zerowej długości, to jednak punkty te tworzą przedział o dodatniej długości 5

PRZYKŁAD 3.4. GP ZLC X jest postaci

f(_Xv_JA(2x-x^:) dla 0<x<2

(0    dla pozostałych x

(o takiej GP mówi się, że jest skoncentrowana na przedziale (02) albo, że przedział (0.2) jest nośnikiem rozkładu ZL X). Wyznaczymy: a) stałą A. b) P(0<;X<l/2), c) P(0<X<l).

a) stałą A znajdujemy z warunku unormowania (3.6):

r

2

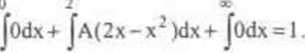
0

2

—x

Stąd 4A/3 = I, czyli A =3/4.

b) Na podstawie równości (3.5) znajdujemy (por. rys 3.4),

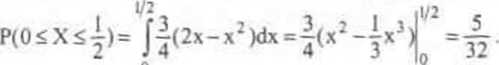
0

c) Krzywa gęstości jest symetryczna względem prostej x=*l. Stąd oraz z warunku unormowania znajdujemy bez całkowania szukane

pr-stwo: P(0<X<1)= 1/2.

y

y

plOo^r)

Ci

x

Rys 3.4.

Rys 3.5.

DYSTRYBUANTA. Niech X będzie ZL dowolnego typu określoną na PP (Q_1<rą.P).

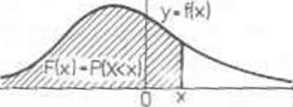
Dystrybuantą ZL X nazywamy funkcję F określoną na całej osi równością:

(3.8) F(x) = P(X<x), xeR