Matematyka 2 37

336 V. Elementy rachunku prawdopotliibicństwa

Jeśli X jest ZLS o punktach skokowych x_k i skokac Pk = P(x_k). to wzór (3.8) przyjmuje następujący postać:

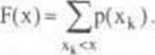
(3.9)

W szczególności, gdy x,,x₂^..^_n są kolejnymi punktami skokowymi, to wzór (3.9) można zapisać w równoważnej postaci:

dla x<x

(3.9)’    F(x)=jF(x_Ł) + p(x_Ł) dla x e(x_k,x_k., >, k = 1,2.....n-1.

1    dla x>x_n

Jeśli X jest ZLC o GP f . to wzór (3.8) przyjmuje następującą postać, (por. rys.3.5),

i

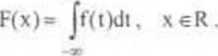
(3.10)

Korzystając z. definicji dystrybuanty dowodzi się TWIERDZENIE 3.1. Dystrybuanta F dowolnej ZL X ma następujące własności FI, F2.....F6:

FI. 0<F(x)<l dla każdego xeR

F2. Dystrybuanta F jest funkcją memalejącą.

F3. lim F(x)=F(-x)=0. lim F(x)=F(+oo)=l

F4. Dystrybuanta F jest funkcją lewostronnie ciągłą, czyli F(Xp)=F(x₀), gdzie F(x₀) oznacza lewostronną granicę dystrybuanty F w punkcie x₀.

F5. F(x₃)-F(x,)=P(x,<X<x₃) dla x,<x_;.

F6. F(xÓ)-F(x₀)=P(X=x„) dla dowolnego x₀ gR

Własności FI-F6 to warunki konieczne na to.-by funkcja F mogła być dystrybuantą. Okazuje się, że warunki F2, F3, F4 również wystarczają na to, aby z góry zadana funkcja F była dystrybuantą. Prawdziwe jest bowiem

TWIERDZENIE 3.2. Jeżeli funkcja F określona na całej osi ma własności F2, F3, F4 sformułowane w twierdzeniu 3.1. to jest ona dys-trybuantą.

Własności FI-F6 dotyczą ZL dowolnego typu. Załóżmy teraz, że p jest dystrybuantą ZLC X. Można oczekiwać, żc własności ic mogą przybrać teraz bardziej szczegółową postać lub mogą pojawiać się nowe. Traktuje o tym następujące

TWIERDZENIE 3.3. Dystrybuanta F ZLC ma następujące własności FC1, FC2, FC3:

FCI. Gdy x,<x,. to

Fix_:)-F(x₁) = P(x,<X<x₂)=P(x_l<X<x₂)=P(x₁^X<x₂)=P(x, <X<x₃) FC2. Dystrybuanta ZLC jest funkcją ciągłą na całej osi.

FC3. Jeśli F jest dystrybuantą ZLC X. to funkcja f postaci | F'(x) dla tych x, dla których istnieje pochodna F'(x)

^X ” [0 dla pozostałych x

jest GP ZL X.

Własność FC3 z twierdzenia 3.3 umożliwia wyznaczanie GP f. gdy w i e m y . że ł- jest dystrybuantą ZLC Z następnego twierdzenia wynika sposób rozpoznawania dystTybuanty ZLC

TWIERDZENIE 3.4. Jeżeli F jest dystrybuantą ZL X i funkcja f określona równością postaci (3.11) spełnia warunek unormowania (3.6), to X jest ZLC oraz funkcja f jest jej GP.

PRZYKŁAD 3.5. Wyznaczymy dystrybuantę ZLS X z przykładu 3.3 Jej funkcja pr-stwajest postaci:

*k	0	1	2	3
Pk=p(*k)	1/8	3/8	3/8	1/8

Wykorzystamy wzór (3.9)’. Ponieważ ZLS X ma cztery punkty skokowe, w ięc jej dystrybuantę należy rozpatrywać w pięciu przedziałach, na jakie dzielą one oś 0x. Kolejno obliczamy:

dla x£0    F(x)= P(X<x) = P(X<0)=F(0)-0,

dla 0<x<l

F(x)=l*(X<x)=P(X<l)>F(l)=F(0) + p(0) = 0+|=i. dla l<x<2

F(x)=P(X<x) = P(X<2)=F(2)»F(l)+p(l)=j+|=|.