0191

192

III. Pochodne i różniczki

Rezultat ten ma różne zastosowania. Z jego pomocą możemy wyrobić sobie na przykład pojęcie o dokładności zwykłego suwaka logarytmicznego o długości skali 25 cm=250 mm. Przy odczytywaniu lub ustawianiu okienka można omylić się mniej więcej o 0,1 mm w jedną lub drugą stronę, co odpowiada błędowi logarytmu.

o    0.1

<5y= —=0,0004.

Stąd według naszego wzoru

<Jx_0,0004 ~ 0,4343

=0,00092 » 0,001 .

Dokładność względna we wszystkich częściach skali jest ta sama.

Przykład 3. Przy obliczaniu kąta ę z tablic logarytmiczno-trygonometrycznych powstaje pytanie, z jakich tablic wygodniej jest korzystać — z tablic sinusów, czy tangensów. Niech

,yi=logiosin$> i    = logio tg ?»;

będziemy uważali, że błędy maksymalne Sy₂ i Sy₂ są równe (niech będą równe, powiedzmy, połowie ostatniego znaku dziesiętnego mantysy). Jeśli oznaczymy odpowiednie błędy maksymalne kąta ę przez Si ę i S₂ę, to otrzymamy jak wyżej

M

M

tak, że

Syi—-• cos <p ■ 6_tę , Sy₂—-• sec ę • S₂

sm ę    tg p

S₂q>—ói pcos^s q><Si <p .

Okazuje się w ten sposób, że przy jednakowych błędach w logarytmie tablica tangensów daje mniejszy błąd dla kąta niż tablica sinusów i jest tym samym wygodniejsza 0).

B

(13)

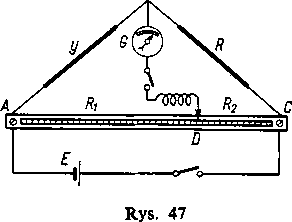
Przykład 4. Jako ostatni przykład rozpatrzymy zagadnienie dokładności pomiaru niewiadomego oporu y za pomocą mostka Wheatstone’a (rys. 47). Kontakt ruchomy D przesuwa się wzdłuż cechowanej linijki AC dopóty, dopóki galwanometr G nie wykaże nieobecności prądu. Opór y wyznaczamy według wzoru

Rx

y=-

gdzie a=AC, x=AD, R — opór wiadomy rozgałęzienia BC. Na podstawie wzoru (12) otrzymujemy

,    aR

Sy=\-1 * Sx=--j • Sx ;

\a—x/_x (a—x)

jeśli podzielimy obie strony ostatniej równości przez odpowiednie strony równości (13), to otrzymamy następujące wyrażenie na (maksymalny) błąd względny wielkości y:

Sy crSx y x(a-x)

(‘) Przy tych obliczeniach zakładaliśmy, że kąty wyrażone są w radianach, jednak wyniki te pozostaną słuszne oczywiście niezależnie od tego, w jakich jednostkach mierzymy kąty.