021

21

11 Prawa wielkich liczb i symulacje

Odka obliczona mtkodą Monte Codo

Przykład. Obliczyć całkę

i

„-sin² kx

1 + X²

o

(wykres funkcji podcałkowej na rysunku 2).

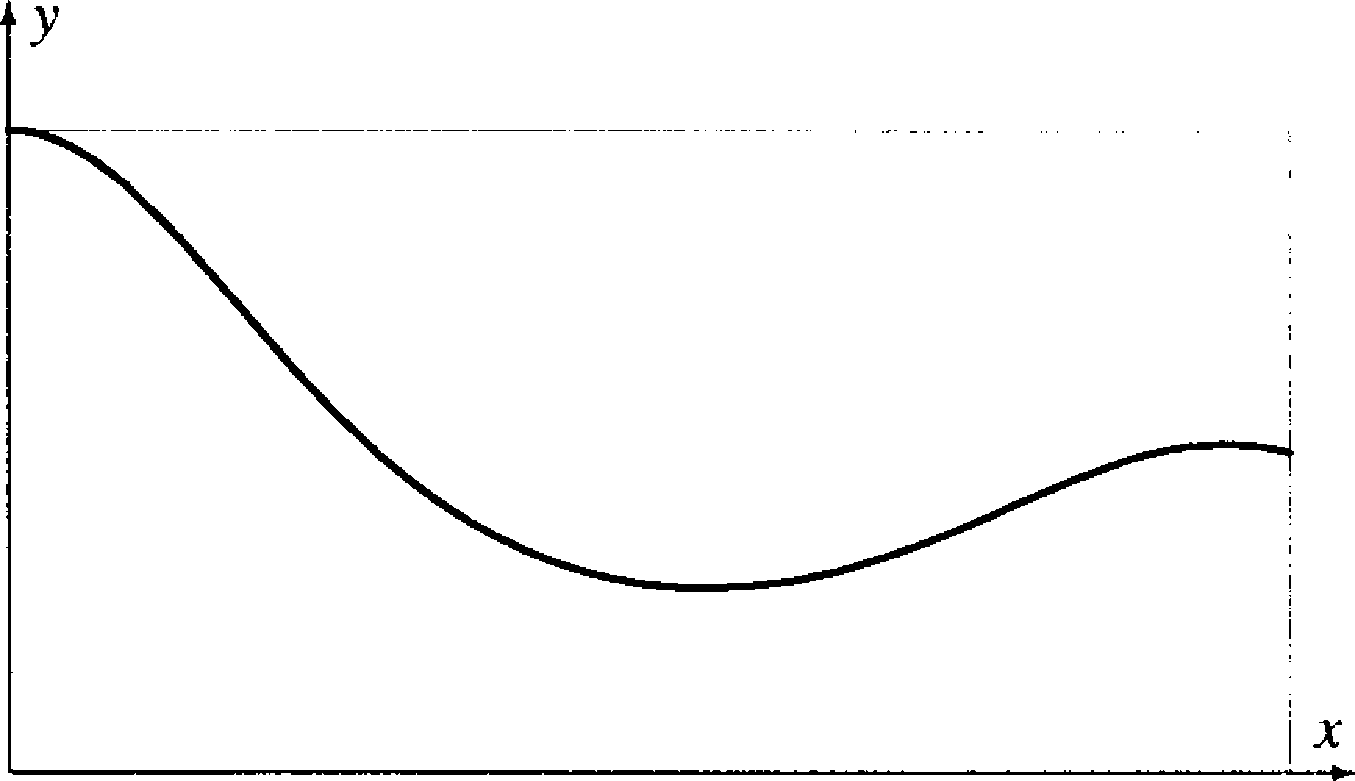
Rysunek 2: Wykres funkcji z przykładu

Całki tej nie da się obliczyć elementarnie. Metoda Monte Carlo polega na otrzymaniu ciągu n niezależnych punktów (x_i,y_i) z prostokąta [0,1] x [0,1], a następnie obliczeniu liczby k tych punktów    które spełniają nierówność

g- sin 7tx_i

1 +Xi

Ponieważ maksimum funkcji podcałkowej wynosi 1, więc I = Pr (A) dla A będącego obszarem pod krzywą i Q będącego prostokątem. Na podstawie prawa wielkich liczb (twierdzenia 1.2.1 i 1.2.2) można więc przyjąć, że

i

1

. 2

* —sin a:

1 +x²

3

0

Symulacja w TUrbo Pascalu

Procedura całka.pas oblicza tę całkę metodą Monte Carlo. Procedura ta dla 5 kolejnych przebiegów³ dała liczby:

0.5320, 0.4870, 0.5340, 0.4610, 0.5160, a ta sama procedura, ale dla n = 10000 dała 0.5045, 0.5011, 0.5046, 0.5006, 0.5045,

podczas gdy prawdziwa wartość całki (obliczona numerycznie przy pomocy programu Mathematica) jest równa 0,503498 z dokładnością do 6 cyfr dziesiętnych.

³Dla następnych 5 przebiegów dostanie się zapewne inne liczby