063

63

3,1. Nierówność Czebyszewa i prawa wielkich liczb

Przykład. Rozpatrzmy ponownie ostatni przykład, tzn. X jest liczbą sukcesów w 20 próbach, gdzie prawdopodobieństwo sukcesu w jednej próbie wynosi p = 0.4, q = 1 — p. Niech

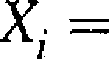
1

0

gdy sukces w i-tej próbie, gdy porażka w i-tej próbie.

oraz X- = X_i — p, X' — X[ i- Xó -\----4- X^fn — X — m, gdzie m — np. Wtedy

EX/ = 0, K — max{p_}q}, a^{1 2} = D²X[ — pq. Przyjmując we wzorze (3.1.3) 4 — tOyfn — tyjpqn = \/20 ■ 0.4 • 0.6 otrzymujemy t = 4/\/20 ■ 0.4 ■ 0.6 = 1.82574, skąd po podstawieniu wartości liczbowych

u — 2exp

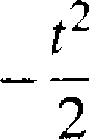
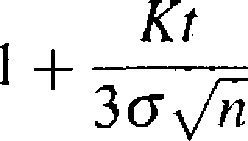
— 0.286133,

a więc

Pr(4<X< 12) — Pr(|X — m\ ^ 4) = l-Pr(|X-m| >4)

> 1 — Pr(|X — m\ >4) ^ 1 - « = 0.713867.

Oszacowanie Czebyszewa dało oszacowanie nieco gorsze, równe 0.7.

3.1.2. Prawa wielkich liczb

Z nierówności Czebyszewa można wyprowadzić słabe prawo wielkich liczb dla zmiennych losowych. Takie sformułowanie prawa wielkich liczb jest ogólniejsze, niż sformułowanie dla zdarzeń, jak to zrobiono w punkcie 1.2.1.

Słabe prawo wielkich liczb

Twierdzenie 3.1.4.

Niech XpX₂,... będzie ciągiem niezależnych zmiennych losowych o tym sa-

r-y

mym rozkładzie, o wartości oczekiwanej m i wariancji 0 < c < °°. Wtedy dla każdego £ > 0 mamy

lim Pr

n—>oo

Xy + X^ + X_n

— m

<£ = 1

n

(3.1.4)

n

co daje tezę twierdzenia dla n

Pr (|X

n

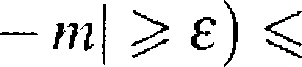
oo.

a

2

n£

2 ’

1

Dowód. Dla skrócenia zapisu oznaczmy

v _    ^-----

A _n —    .

n

2

Z niezależności zmiennych losowych X- wynika, że EX„ — m, a także D²X,j = o²fn. Przyjmując £ — ta w nierówności Czebyszewa (3.1.2), można napisać, że