061

3. Twierdzenia graniczne

3.1. Nierówność Czebyszewa i prawa wielkich liczb

3.1.1. Nierówności Markowa i Czebyszewa

Hierówność

Markowa

Dwa podane dalej oszacowania, wykorzystywane są w dowodach wielu twierdzeń. Kolejno sformułujemy nierówności Markowa¹² i Czebyszewa¹².

Twierdzenie 3.1.1.

Jeśli Pr(X > 0) = 1 oraz EX < oo to dla każdego k > 0 zachodzi nierówność

Pr (X^k) < |eX\

k

(3.1.1)

Dowód. Ponieważ Pr(X > 0) = 1 to F(x) = 0 dla x < 0. Zatem

oo

co

EX — / xdF(x) = / xdF(x) 4- / xdF(x)

o

o

oo

co

^ j xdF(x) ^k j dF(x) = k Pr(X > k), k    k

skąd wynika teza twierdzenia.

i

Nierówność Twierdzenie 3.1.2.

Czebyszewa _Jeśn EX = m, 0 < a² = D²X < oo, to dla każdego t > 0

Pr(|X — ml ^ t) ^

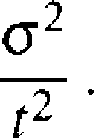
(3.1.2)

I ^

Andriej Andriejewicz Marków (1856 - 1922), matematyk rosyjski.

¹³Pafnucy Lwowicz Czebyszew (1821 - 1894), matematyk i mechanik teoretyk rosyjski.