059

59

3.2. Centralne twierdzenie graniczne

a)    korzystając z nierówności Czebyszewa,

b)    korzystając z twierdzenia Moivre’a-Laplace’a dla n = 9000.

Zinterpretować te oszacowania.

Zadanie 3.2.9.

Czy można zastosować twierdzenie Lindeberga-Levy’ego dla ciągu niezależnych zmiennych losowych o gęstościach

Zadanie 3.2.10.

Zmienne losowe X_} ,X₂, ■ ■ ■ ,X₁₀₀ są niezależne o jednakowym rozkładzie wykładniczym z parametrem X = 4. Dla

100

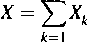
obliczyć przybliżoną wartość wyrażenia Pr(X > 30).

Zadanie 3.2.11.

Obliczyć w przybliżeniu prawdopodobieństwo, że partia 100 elementów, z których każdy ma czas pracy 7] (i = 1,2,...,100) wystarczy na zapewnienie pracy urządzenia przez łącznie 100 godzin, gdy wiadomo, że E7] = 1 oraz D²7] — 1.

Zadanie 3.2.12.

Tygodniowe wypłaty z pewnego funduszu są niezależnymi zmiennymi losowymi o rozkładzie wykładniczym z tym samym parametrem X =    . Obliczyć prawdopodobień

stwo, że łączna wypłata z tego funduszu w okresie roku, tzn. 52 tygodni, przekroczy 70000 zł.

Zadanie 3.2.13.

Zmienne losowe X, ,X₂, ■ ■ • ,X₆₀ mają rozkład jednostajny na odcinku [1,3]. Niech

60

Obliczyć przybliżoną wartość wyrażenia Pr(l 18 < X < 123).

Zadanie 3.2.14.

Zmienne losowe X_l,X₂,...,X_|00 są niezależne o jednakowym rozkładzie Poissona z parametrem X =2. Obliczyć przybliżoną wartość wyrażenia

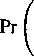
190 < J2^Xi < 220 .

100

i=i