061
61
3.2. Centralne twierdzenie graniczne
Zadanie 3.2.21.
Czas pracy lampy pewnego typu ma rozkład wykładniczy o średniej 900 godzin. Ile lamp trzeba mieć w zapasie, aby z prawdopodobieństwem 0.99 wystarczyło ich na 4 lata nieprzerwanej pracy? Zakładamy, że spalona lampa jest natychmiast wymieniana na nową.
Zadanie 3.2.22.
Niech x2 ma rozkład chi-kwadrat o n stopniach swobody. Wyznaczyć Pr (x2 < Xl) dla n = 35 i n = 43 oraz dla %a — 18.06, Xa = 27.10.
Zadanie 3.2.23.
Wyznaczyć kwantyl rzędu 0.57 dla rozkładu chi-kwadrat o 31 stopniach swobody. Zadanie 3.2.24.
Niech t ma rozkład r-Studenta o n stopniach swobody. Wyznaczyć Pr (7 >0.73) gdy n = 33 i n = 41.
Zadanie 3.2.25*.
Na ulicy stoi sprzedawca hot dogów. Załóżmy, że każdy z mijających go przechodniów kupuje jednego hot doga z prawdopodobieństwem 0.05. Niech X oznacza ilość ludzi mijających go aż do chwili, gdy sprzeda on 50 porcji hot dogów. Znaleźć asymptotyczny rozkład zmiennej losowej X.
Zadanie 3.2.26.
Niech Xk będzie ciągiem niezależnych zmiennych losowych, Pr yXk —2k) =
Pr [Xk = 2kj = 1 /2. Sprawdzić, czy dla takiego ciągu spełnione są założenia twierdzenia Lapunowa.
Zadanie 3.2.27.
Niech Xk będzie ciągiem niezależnych zmiennych losowych, Xk ~ N(0, k). Sprawdzić, czy dla takiego ciągu spełnione są założenia twierdzenia Lapunowa. Jeśli są, to wyznaczyć
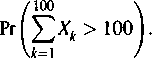
Wyszukiwarka
Podobne podstrony:
stat Page@ resize 40 3.6 Testy statystyczne przy czym niech np. a = 0,05. Korzystając z centralnego
• prawo wielkich liczb • centralne twierdzenie graniczne
55 3.2. Centralne twierdzenie graniczne3.2. Centralne twierdzenie granicznePrzykładyPrzykład
57 3.2. Centralne twierdzenie graniczne Korzystając z z twierdzenia Lindeberga-Levy’ego
59 3.2. Centralne twierdzenie graniczne a) korzystając z nierówności Czebyszewa, b
66 3. Twierdzenia graniczne3.2. Centralne twierdzenia graniczne3.2.1. Twierdzenie Lindeberga-Levy’eg
67 3.2. Centralne twierdzenia graniczne gdzie reszta R^{t) spełnia warunek R^(t)/t2 —* O dla t —» 0.
69 Centralne twierdzenia graniczne3.2.2. Twierdzenie Lapunowa Założenia twierdzenia 3.2.1 można tak
57 3.2. Centralne twierdzenie graniczne Korzystając z z twierdzenia Lindeberga-Levy’ego
Przytocz i wyjaśnij centralnie twierdzenie graniczne i wniosek z tego twierdzenia. Centralne twierdz
więcej podobnych podstron