067
67
3.2. Centralne twierdzenia graniczne
gdzie reszta R^{t) spełnia warunek R^(t)/t2 —* O dla t —» 0. Ze wzoru (3.2.2) otrzymujemy
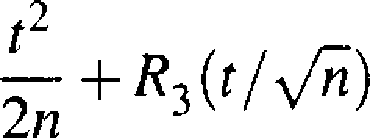
n
oraz
—»oo
lim nR3(t2/n) = 0.
Podstawiając w = t2/2n + RJt/y/n) otrzymujemy
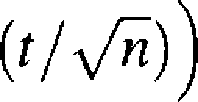
\nęZft(t) = nln(l — u) ~n t2/2n-\-R3 = -t2/2 + w/?3(r/v/n),
skąd
lim ln©7 (t) — —t2 i2,
rt—>oo r x * 1
czyli
lim (p7 (f)

Przyjmując w twierdzeniu 3.2.1 Pr(X. = 1) = p i Pr(Xi = 0) = 4 dla p 4* = 1, otrzymujemy następujące twierdzenia.
Twierdzenie 3.2.2. (Moivreya-Laplace'a)
Niech Pr(7,j = fc) = 6(/r,/:,/?), czyli Yn ma rozkład dwumianowy z parametrami nip. Wtedy
lim Pr
Yn ~ np
\/npą
<x
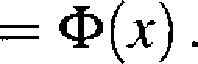
(3.2.3)
Asymptotyczna Własność wyrażoną w twierdzeniu 3.2.2 można interpretować tak, że wy-normalność standaryzowana zmienna losowa o rozkładzie dwumianowym
y = Yn~nP ^/npq
ma rozkład w przybliżeniu normalny N(0,1) dla dużych n albo że Yn ma w przybliżeniu rozkład normalny N(np, yjripą). Mówimy też, że Yn ma rozkład asymptotycznie normalny z parametrami np i yjnpą. Dokładność takiego przybliżenia podaje następujący wzór:
sup
x€R
Pr
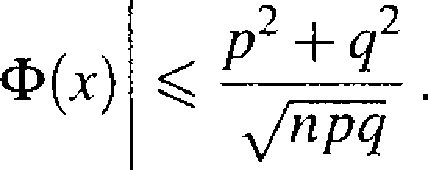
Wyszukiwarka
Podobne podstrony:
stat Page@ resize 40 3.6 Testy statystyczne przy czym niech np. a = 0,05. Korzystając z centralnego
• prawo wielkich liczb • centralne twierdzenie graniczne
55 3.2. Centralne twierdzenie graniczne3.2. Centralne twierdzenie granicznePrzykładyPrzykład
57 3.2. Centralne twierdzenie graniczne Korzystając z z twierdzenia Lindeberga-Levy’ego
59 3.2. Centralne twierdzenie graniczne a) korzystając z nierówności Czebyszewa, b
61 3.2. Centralne twierdzenie graniczneZadanie 3.2.21. Czas pracy lampy pewnego typu ma rozkład wykł
66 3. Twierdzenia graniczne3.2. Centralne twierdzenia graniczne3.2.1. Twierdzenie Lindeberga-Levy’eg
69 Centralne twierdzenia graniczne3.2.2. Twierdzenie Lapunowa Założenia twierdzenia 3.2.1 można tak
57 3.2. Centralne twierdzenie graniczne Korzystając z z twierdzenia Lindeberga-Levy’ego
Przytocz i wyjaśnij centralnie twierdzenie graniczne i wniosek z tego twierdzenia. Centralne twierdz
więcej podobnych podstron