066

66

3. Twierdzenia graniczne

3.2. Centralne twierdzenia graniczne

3.2.1. Twierdzenie Lindeberga-Levy’ego

W tym punkcie przedstawimy dwa szczególne przypadki twierdzeń, należących do całej rodziny twierdzeń granicznych, najważniejszych w rachunku prawdopodobieństwa, a znanych pod wspólną nazwą centralnego twierdzenia granicznego. Twierdzenia te mówią, że przy pewnych założeniach, rozkład wy standaryzowanej sumy n zmiennych losowych dąży do rozkładu N(0,1) dla n —» oo. Twierdzenia tu podane są związane są z nazwiskami Moivre’a¹⁴, Laplace’a¹⁵, Lindeberga i Levy’ego.¹⁶ Są to twierdzenia historycznie najstarsze ze wspomnianej już rodziny twierdzeń granicznych.

Twierdzenie 3.2.1. (Linde be rga-Levy’ego)

D²X < °o =

istnieje

wariancja

Niech X₁,X₂,...,X„ będą niezależnymi zmiennymi losowymi o tym samym rozkładzie, wartości oczekiwanej m = EX i wariancji 0 < o² = D²X <[ OO. Wtedy

lim Pr

Xj T^- X₂ “I^- • • • “b X_n — nm

Gsfn

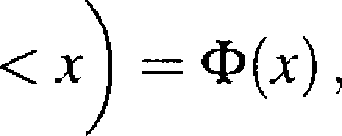
(3.2.1)

gdzie <£>(*) jest dystrybuantą rozkładu normalnego N(0,1).

Dowód. Funkcja charakterystyczna rozkładu normalnego N(0,1) ma postać

ę(t) — e^_/ /². Oznaczmy przez <p_x(t) funkcję charakterystyczną zmiennej losowej X/ = X- — m, a przez (f) funkcję charakterystyczną zmiennej losowej

__x;+x^ + .--+x,;

—

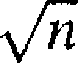
a

występującej po lewej stronie wzoru (3.2.1). Uwzględniając znane już własności (punkt 2.5.1) funkcji charakterystycznej otrzymujemy, że

(3.2.2)

Zastosujemy teraz do funkcji (p_x(t) wzór Maclaurina. Ponieważ <p_x(0) ⁼ <p_x(0) = 0 oraz (p_x(0) = —a², więc

(0 = ¹ - ^²f² + ₃(0.

¹⁴Abraham de Moivre (1667 - 1754), matematyk angielski, zajmował się m.in. rachunkiem prawdopodobieństwa, a także teorią liczb zespolonych (wzór Moivre’a).

^l5Pierre Simon de Laplace (1749 - 1827), francuski astronom, fizyk i matematyk, jeden z twórców rachunku prawdopodobieństwa.

¹⁶Paul Pierre Levy (1886 - 1971), matematyk francuski.