0065

66

I. Teoria granic

nazywamy logarytmami naturalnymi i oznaczamy je znakiem ln bez wskazania podstawy. W badaniach teoretycznych posługujemy się wyłącznie logarytmami naturalnymi C¹).

Wspomnijmy, że zwykłe logarytmy dziesiętne związane są z logarytmami naturalnymi znanym wzorem:

logx=lnx-M,

gdzie M jest modułem przejścia, równym

M = log e = — = 0,434294...;

^B ln 10

wzór ten łatwo otrzymać, logarytmując przy podstawie 10 tożsamość

x = e^b>x.

37. Przybliżone obliczenie liczby e. Powróćmy do równości (6). Jeżeli ustalimy k i przyjmując n>k, pominiemy wszystkie wyrazy dalsze za (k + l)-szym, to otrzymamy nierówność

^xn > 2 +

1

2!

+... +

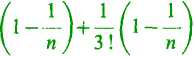
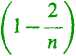
k !

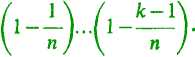
Przejdźmy teraz do granicy przy «-¹• oo; ponieważ wszystkie nawiasy mają jako granicę 1, otrzymujemy

1    1    1

e>2+    —=y¹.

2!    3!    k\ ■

Nierówność ta jest słuszna przy każdym k naturalnym. Tak więc mamy

x_n<y_n^e,

skąd widać (na podstawie twierdzenia 3°, 28), że również

lim>_n=e.

Zauważmy przy okazji, że y„ jest (n+ l)-szą sumą częściową dla szeregu nieskończonego [25, 9)]

n :

1! 2!

i napisany właśnie związek graniczny pokazuje, że e jest sumą tego szeregu; mówimy także, że liczba e rozwija się w ten szereg i piszemy

1 1 1

e=l+ •- +    + —. + ...

1

Logarytmy te nazywają niekiedy logarytmami neperowskimi od nazwiska szkockiego matematyka J. Nepera (Napier, XVI - XVII w). Sam Neper nie znał pojęcia podstawy logarytmów (budując je po swojemu, na innej zasadzie), ale jego logarytmy odpowiadają logarytmom o podstawie bliskiej l/e. Podstawę bliską e mają logarytmy współczesnego mu J. Burgiego.