069

69

Centralne twierdzenia graniczne

3.2.2. Twierdzenie Lapunowa

Założenia twierdzenia 3.2.1 można tak zmodyfikować, nie wymagać jednakowych rozkładów dla zmiennych losowych X_k. W zamian za to wprowadza się inne ograniczenia.

Twierdzenie 3.2.4. (Lapunowa¹¹)

Niech X_ł,X₂,... ,X_rt będą niezależnymi zmiennymi losowymi o skończonych trzecich momentach. Oznaczmy

n

n

Jeśli

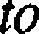
B_n = T D²x_k oraz C„ = £ E^-EY,

lim

n

©O

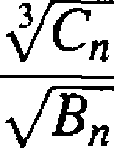
k= 1

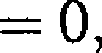
3

(3.2.8)

(3.2.9)

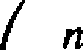
n

lim Pr

Yl—*co

\

h=\    k=1

\

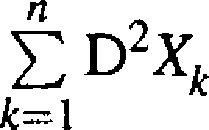
< X

)

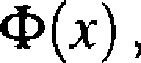
(3.2.10)

gdzie &(x) jest dystrybuantą rozkładu normalnego N(0,1).

Jeżeli zmienne losowe X_k mają ten sam rozkład i istnieje trzeci moment, to B_n i C_n określone wzorem (3.2.8) mają postać B_n — a²n i C_n = c³n, gdzie c³ = E\X_k — EX_jt| nie zależy od k. Zatem założenie (3.2.9) przybiera postać

lim = lim nj^n ^1//2 = lim n = 0

n—(Jy/łl    n—►<»    n—*o°

i z twierdzenia 3.2.1 wynika (przy dodatkowym założeniu o istnieniu trzeciego momentu) twierdzenie 3.2.4

3.2.3. Zadania

3.2.1. Korzystając z twierdzenia Lindeberga-Lćvy’ego pokazać, że rozkład chi-kwadrat o n stopniach swobody jest asymptotycznie normalny N(w, \/2n).

¹⁷ Aleksandr M. Lapunow (1857 - 1918), rosyjski matematyk i mechanik teoretyk.