0244

245

§ 1. Badanie przebiegu funkcji

Jasne jest stąd, że w punkcie x — —2 funkcja ma maksimum, w punkcie x= —0,8 ma minimum, a w punkcie x = \ nie ma w ogóle ekstremum.

Zwykle jednak postępujemy inaczej, nie podstawiamy do pochodnej wartości konkretnych. Zacz

i 5jc+4 dla x— —2 ma znak

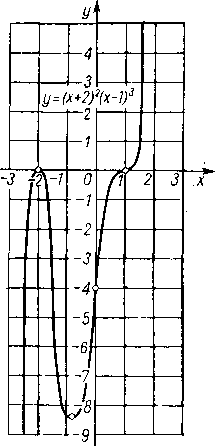
Rys. 57

nijmy od x= —2. Iloczyn dwóch ostatnich czynników pochodnej (x—l)² minus, a więc wskutek ciągłości zachowuje ten sam znak również w pobliżu tego punktu (zarówno z lewej strony, jak i z prawej). Natomiast czynnik x+2 zmienia znak z minusa na plus, gdy x wzrastając przechodzi przez wartość —2, pochodna zmienia więc znak z plusa na minus i funkcja ma maksimum. Dla x= —j (i w pobliżu tej wartości) pierwsze dwa czynniki pochodnej mają znak plus; ostatni natomiast czynnik 5x+4 (a razem z nim cała pochodna) przy przejściu przez tę wartość zmienia znak z minusa na plus; funkcja ma tu minimum. Wreszcie przy przejściu przez wartość x—l nie tylko pierwszy i trzeci czynnik zachowują znaki, ale i drugi czynnik też, kwadrat bowiem jest zawsze dodatni; ekstremum w tym punkcie nie ma.

Znając punkty x, w których dana funkcja ma ekstrema, możemy łatwo obliczyć również same wartości ekstremalne; maksimum /(—2)=0, minimum /(—0,8)« — 8,40.

Na rys. 57 widzimy wykres ilustrujący przebieg tej funkcji (*).

2) Znaleźć ekstrema funkcji /(*)=sin³ x+cos³ x.

Ponieważ funkcja ta ma okres 2jc, wystarczy rozpatrzyć te wartości x, które są zawarte w przedziale <0, 2n>. Pochodna tej funkcji istnieje wszędzie:

f\x) — 3 sin²* cos x~3 cos² x sin x=3 sin x cos x (sin x—cos x). Pierwiastki pochodnej (punkty stacjonarne) będą w tym wypadku następujące:

0,r*.

Przy przejściu przez x=0 czynnik sin x zmienia znak z minusa na plus, pochodna zaś zmienia znak z plusa na minus, ponieważ ostatnie dwa czynniki zachowują w pobliżu x=0 znak minus; mamy tu więc maksimum. Czynnik sin x—cos x dla x=in równa się zeru i przy przejściu przez ten punkt zmienia znak z minusa na plus. To samo będzie z pochodną, ponieważ pierwsze dwa czynniki są dodatnie;

mamy więc tutaj minimum. Analogicznie badamy również pozostałe punkty stacjonarne, wszystkie one będą po kolei punktami maksimum i minimum.

Podstawiając je otrzymamy wartości ekstremalne: maksima: /(0)=/(2tt)=l, /({n)-l, /<!*)= ~ V**-0,71. minima: /(jtt)=| -J2x0jl, f(n)= -1, /(|tt)= -1.

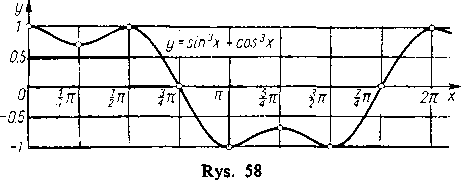
Wykres funkcji przedstawiony jest na rys. 58 (porównaj ustęp 147, 1)).

(') W tym i w następnych przykładach ilustrujemy przebieg funkcji za pomocą wykresu, samo jednak zagadnienie zbudowania wykresów rozpatrzymy szczegółowo dopiero w§ 3. (Patrz w szczególności 149,3).