0250

251

§ 1. Badanie przebiegu funkcji

Na przykład dla funkcji f(x)=e*+e~^x+2cos* punkt x=0 jest punktem stacjonarnym, gdyż w punkcie tym jest równa zeru pochodna

f'{x)—e^x —e~*—2sin* .

Mamy dalej

f"(x)=e*+e~*—2cos.x ,    /"(0)=0 ;

f"'(.x)=e^x-e-^x+2sinx ,    /"’(0)=0 ;

f⁽ⁱ\x)=e^x+e~^x+2cosx,    /'*>(()) =4 .

Ponieważ pierwszą nie znikającą pochodną jest pochodna rzędu parzystego, mamy tu ekstremum, a mianowicie minimum, bo /⁽⁴⁾(0)>0.

Uwaga. Chociaż wyprowadzone wyżej kryterium rozwiązuje zagadnienie ekstremum w dosyć szerokiej klasie przypadków, ale teoretycznie rzecz biorąc nie jest ono uniwersalne: funkcja nie będąca tożsamościowo stałą może mieć w otoczeniu badanego punktu pochodne wszystkich rzędów, które jednak w tym punkcie wszystkie jednocześnie znikają.

Rozpatrzymy jako przykład następującą funkcję podaną przez Cauchy’ego:

f(x)—e~^llxl (dlax?ŁO), /(0j=0.

Dla x/0 ma ona pochodne wszystkich rzędów

f(.x)=-_le ^11x1,    /"(*) = (-4i + ~i\e ^11x2,

X    \ X X /

ogólnie

(9)

/^<n,(x)=P,,^tr^Ux2 (« = 1,2,...),

gdzie P„(z) jest wielomianem stopnia 3n. Słuszność tego ogólnego wzoru łatwo można sprawdzić metodą indukcji matematycznej.

Wykażemy obecnie, że także w punkcie x=0 dana funkcja ma pochodne wszystkich rzędów, przy czym wszystkie one są równe zeru. Rzeczywiście, mamy przede wszystkim

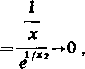
gdy x->0 ('),

m-m

x

tak że /'(0)=0. Załóżmy, że podlegające dowodowi twierdzenie jest słuszne dla wszystkich pochodnych do rzędu n włącznie. Wtedy (patrz (9))

/<»>(*) _/<»

x

0,

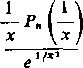
gdy x~»0,

ponieważ licznik jest sumą wyrazów kształtu ctx^m. Tak więc również /⁽ⁿ⁺¹⁾(0)=0. Zgodnie z zasadą indukcji matematycznej twierdzenie zostało udowodnione w zupełności.

Chociaż jest rzeczą bezpośrednio oczywistą, że dana funkcja ma w punkcie x—Q minimum, nie można stwierdzić tego za pomocą badania jej kolejnych pochodnych w tym punkcie.

0) Przypominamy, że e‘ przy z-> + oo jest nieskończenie dużą wyższego rzędu niż dowolna potęga z\ tj.

Z

lim ~ —0

t-» + co e

[65]. Tutaj rolę z odgrywa 1 jx² (przy *->0).