0234

235

§ 1. Badanie przebiegu funkcji

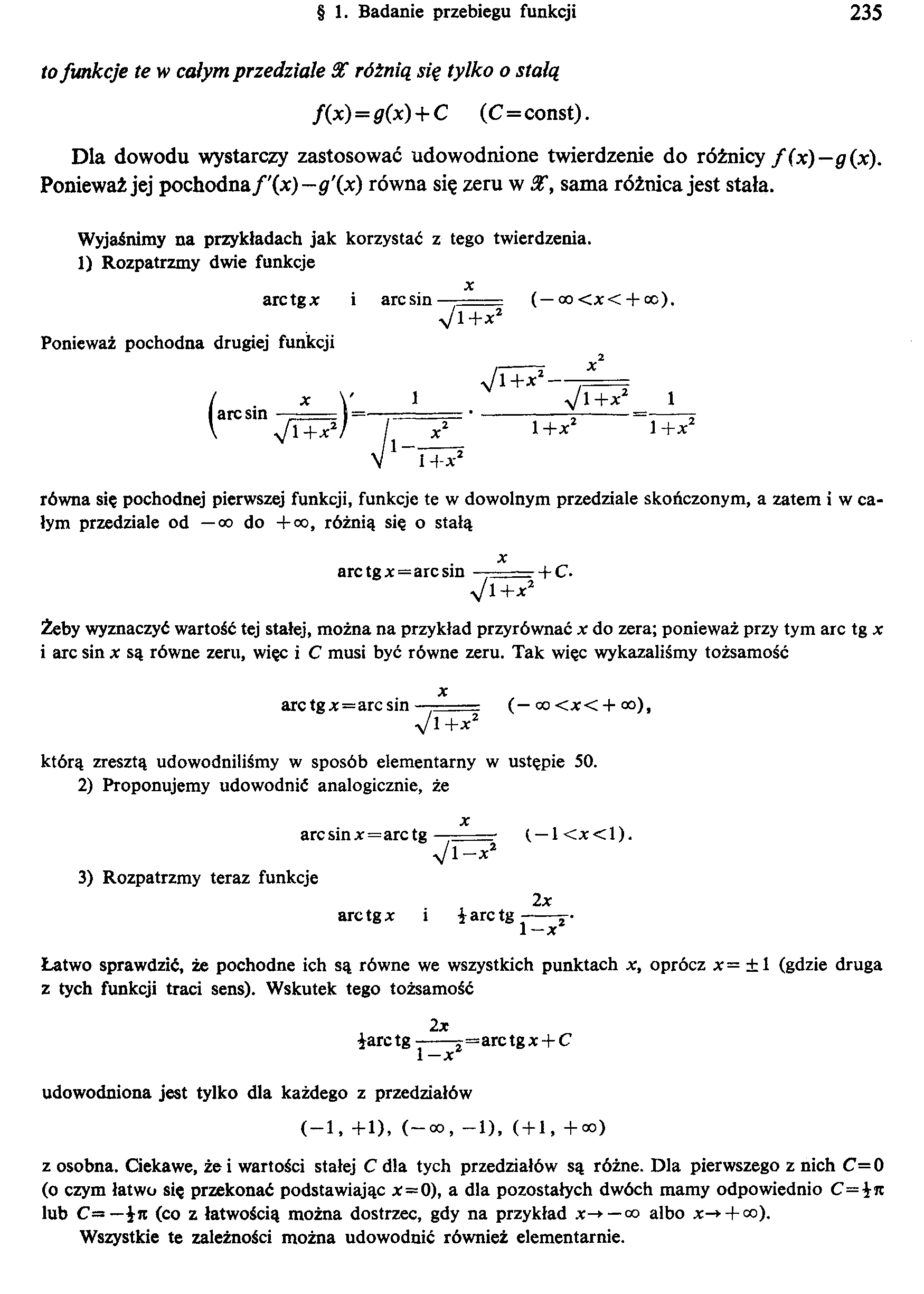
to funkcje te w całym przedziale 3C różnią się tylko o stałą

f(x)=g(x) + C (C=const).

Dla dowodu wystarczy zastosować udowodnione twierdzenie do różnicy f(x)—g(x). Ponieważ jej pochodna f'(x)—g'{x) równa się zeru w 3C, sama różnica jest stała.

Wyjaśnimy na przykładach jak korzystać z tego twierdzenia.

1) Rozpatrzmy dwie funkcje

x

•Jl+x²

arc tg X i arcsin —------ ( —oo <*< + cc).

Ponieważ pochodna drugiej funkcji

I arcsin ■_*___|

u—

V i +*^2—

V l+X²

l+x²

l+x²

równa się pochodnej pierwszej funkcji, funkcje te w dowolnym przedziale skończonym, a zatem i w całym przedziale od — oo do + oo, różnią się o stałą

x

arctgx—arcsin    ■ . 4-C.

y/l+X²

Żeby wyznaczyć wartość tej stałej, można na przykład przyrównać x do zera; ponieważ przy tym arc tg x i arc sin x są równe zeru, więc i C musi być równe zeru. Tak więc wykazaliśmy tożsamość

arc tgx=arc sin —==    (— oo <x< + oo),

y/l+X²

którą zresztą udowodniliśmy w sposób elementarny w ustępie 50.

2)    Proponujemy udowodnić analogicznie, że

x

arc sin x=arc tg —    (. — 1 <x<l).

3)    Rozpatrzmy teraz funkcje

2x

arc tg x i    i arc tg-5--

1 —x

Łatwo sprawdzić, że pochodne ich są równe we wszystkich punktach x, oprócz x= ±1 (gdzie druga z tych funkcji traci sens). Wskutek tego tożsamość

2x

iarc tg-j=arc tg x + C

l—x

udowodniona jest tylko dla każdego z przedziałów

(-1, +1), (-00, -1), ( + 1, +00)

z osobna. Ciekawe, że i wartości stałej C dla tych przedziałów są różne. Dla pierwszego z nich C=0 (o czym łatwo się przekonać podstawiając x=0), a dla pozostałych dwóch mamy odpowiednio C=±n lub C=— Jii (co z łatwością można dostrzec, gdy na przykład x-> — co albo x-> + co).

Wszystkie te zależności można udowodnić również elementarnie.