0240

241

§ 1. Badanie przebiegu funkcji

dla których spełnione są już warunki postaci (6). Na mocy udowodnionego twierdzenia jest więc

£ a',b'_t < 1 ,

i = i

a to jest równoważne z (5).

8) Z nierówności Cauchy’ego-Holdera otrzymujemy od razu jeszcze jedną ważną nierówność, noszącą nazwę nierówności Minkowskiego

(7)    +    ⁺    *>*)•

i=i    i=i    i=i

Jest oczywiście

2>. + M‘=5>,(«, + »,)* ¹ + y^b,(a_t + b,)^k .

<=i    1=1    i=i

Jeśli do każdej z dwóch ostatnich sum zastosujemy nierówność (5), to otrzymamy (*):

I = 1    tm1    1=1    lal    |al

i=i    i=i    i=i

i wreszcie po uproszczeniu przez ostatni czynnik otrzymamy (7).

134. Maksima i minima; warunki konieczne. Jeśli funkcja / (x) określona i ciągła w przedziale <a, by nie jest w nim monotoniczna, to istnieją takie części <«, /?> przedziału (ja, by, w których funkcja osiąga swoją największą lub najmniejszą wartość w punkcie wewnętrznym, tzn. między a a /?. Na wykresie funkcji (rys. 55) przedziałom takim odpowiadają charakterystyczne garby lub wgłębienia.

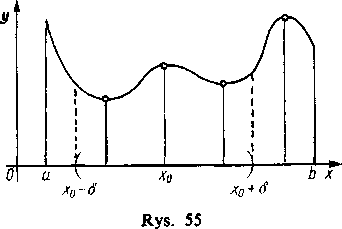
Mówimy, że funkcja f(x) ma w punkcie x₀ maksimum (albo minimum)(²), jeśli istnieje takie otoczenie tego punktu (x₀—S, x₀ + <5), zawarte w przedziale, w którym funkcja jest określona, że dla wszystkich punktów x tego otoczenia spełniona jest nierówność

f(x) < f(x₀)    (albo f(x) >f(x₀)).

Innymi słowy funkcja f{x) osiąga w punkcie x₀ maksimum (minimum), jeśli wartość / (x₀) jest największa (najmniejsza) spośród wartości, które funkcja przybiera w pewnym — choćby i małym — otoczeniu tego punktu. Zwracamy uwagę na to, że w samej definicji maksimum (minimum) leży założenie, że funkcja jest określona po obu stronach punktu x₀.

(’) Przypominamy, że —I— =1.

k k’

(²) Maximum i minimum znaczy po łacinie największe i najmniejsze (w danym wypadku chodzi o największą albo najmniejszą wartość).

16 G. M. Fichtenholz