0246

§ 1. Badanie przebiegu funkcji

247

Wprowadzając pomocniczy kąt ę spełniający warunki

ca    k

z =cos <p ,    =sin

\Ja>² +k²    yjw^+k¹

zapiszemy pochodną w postaci

s'=A \fco² +k² e “cos (cot + ę>).

Jest ona równa zeru w punktach

.LĄY-t.

\    2 / to w

a ponieważ przechodząc przez zero kosinus zmienia znak, łatwo więc zauważyć, że dla tych wartości nasza funkcja rzeczywiście ma maksima dla n parzystych i minima dla n nieparzystych. W porównaniu z sinusoidą ma tu miejsce przesunięcie punktów ekstremalnych na lewo o <pla>.

Łatwo zauważyć, że wszystkie maksima są dodatnie, a minima — ujemne. Jeśli wielkość n-tego ekstremum oznaczymy przez A_n, to

A. A_n +1

₌ gkn/ci>

tak więc wychylenia maleją w postępie geometrycznym.

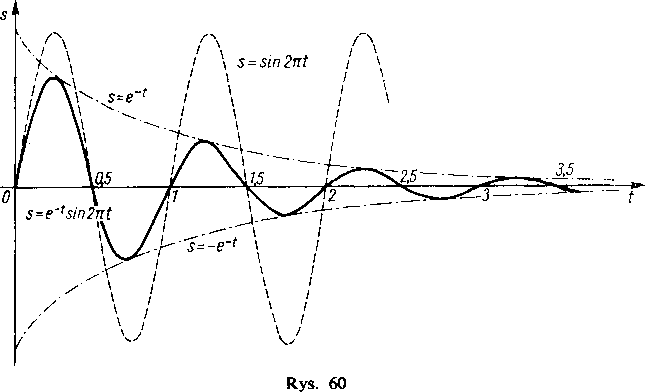
Wykres (w prostym wypadku szczególnym) pokazany jest na rysunku 60. Ruch tego typu nosi nazwę drgań tłumionych.

Uwaga. W większości wypadków występujących w praktyce wyłożona w poprzednim ustępie reguła wystarcza w zupełności do badania wartości „podejrzanych”. Trzeba jednak zdawać sobie sprawę z tego, że mogą być wypadki, w których reguła ta nie może być zastosowana. Będzie tak wtedy, gdy dowolnie blisko badanego punktu znajduje się nieskończony zbiór innych tego rodzaju punktów i pochodna nie zachowuje określonego znaku z jednej lub drugiej strony badanego punktu.

Rozpatrzmy jako przykład funkcję określoną wzorami

f(x)=x² sin— (dla x#0), /(0)=0. x