0252

253

§ 1. Badanie przebiegu funkcji

Uwaga. W zastosowaniach najczęściej spotykamy prosty przypadek, gdy między a i b znajduje się tylko jeden podejrzany punkt x₀. Jeśli w punkcie tym będzie maksimum (minimum), to nie porównując nawet z wartościami funkcji na końcach przedziału możemy powiedzieć, że będzie to właśnie największa (najmniejsza) wartość funkcji w przedziale (patrz rys. 64). Często w podobnych wypadkach łatwiej zbadać maksimum i minimum niż obliczać i porównywać wartości funkcji w różnych punktach (zwłaszcza, gdy w jej skład wchodzą stałe literowe).

Trzeba podkreślić, że to cośmy powiedzieli, można w pełni zastosować także do przedziału otwartego (a, b), jak również do przedziału nieskończonego.

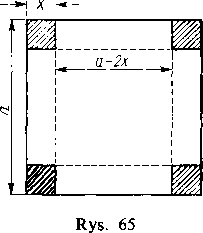
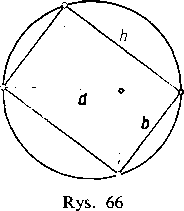
140. Zadania. Wyłożymy teraz w postaci przykładów kilka zadań z różnych dziedzin, których rozwiązanie sprowadza się właśnie do znajdywania największej i najmniejszej wartości funkcji. Zresztą najczęściej interesujemy się nie tyle samymi tymi wartościami, ile punktami (wartościami argumentu), w których funkcja wartości te osiąga.