0236

237

§ 1. Badanie przebiegu funkcji

Konieczność. Jeśli /(x) jest funkcją rosnącą w przedziale 3C, to w myśl twierdzenia 2 mamy /'(*)>0 tak, że warunek 1) jest spełniony. Spełniony jest również warunek 2), bo gdyby pochodna znikła w pewnym przedziale tożsamościowo, to w myśl twierdzenia 1 w przedziale tym funkcja /(x) byłaby stała, co przeczy założeniu.

Dostateczność. Niech będą spełnione warunki 1), 2). Wówczas na podstawie twierdzenia 2 funkcja /(x) jest w każdym razie niemalejąca. Jeśli wziąć w 9C dwie wartości x' i x" (x'<x"), to nie tylko będzie

O)    /(x'K/(x"),

ale również

(2)    f(x')ś:f(x)ś:f(x") dla x należących do przedziału <V, x">.

Udowodnimy, że znak równości w (1) nie może mieć miejsca. Gdyby było /(x')=f(x"), to na mocy (2) otrzymalibyśmy

f(x’)=f(x)=f(x") dla wszystkich x należących do <x', x">,

tzn./(x) byłaby funkcją stałą w przedziale <x', x"> i mielibyśmy f'(x)=0 tożsamościowo w tym przedziale, co przeczy warunkowi 2). Tak więc

/(*') </(*"), gdy x'<x",

tzn. funkcja /(x) jest ściśle rosnąca. Tym samym twierdzenie zostało udowodnione.

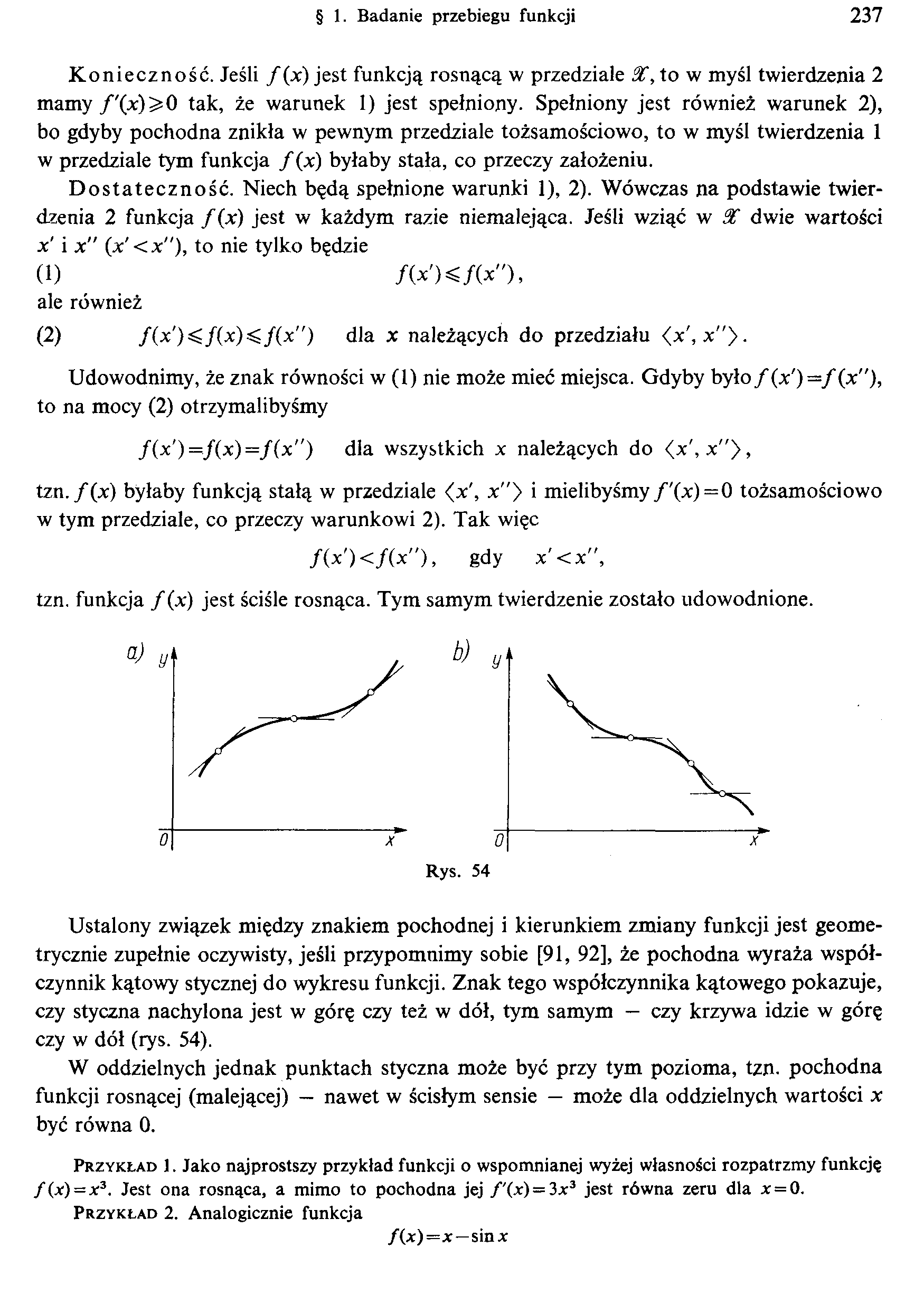
Ustalony związek między znakiem pochodnej i kierunkiem zmiany funkcji jest geometrycznie zupełnie oczywisty, jeśli przypomnimy sobie [91, 92], że pochodna wyraża współczynnik kątowy stycznej do wykresu funkcji. Znak tego współczynnika kątowego pokazuje, czy styczna nachylona jest w górę czy też w dół, tym samym — czy krzywa idzie w górę czy w dół (rys. 54).

W oddzielnych jednak punktach styczna może być przy tym pozioma, tzn. pochodna funkcji rosnącej (malejącej) — nawet w ścisłym sensie — może dla oddzielnych wartości x być równa 0.

Przykład 1. Jako najprostszy przykład funkcji o wspomnianej wyżej własności rozpatrzmy funkcję /(x) = x³. Jest ona rosnąca, a mimo to pochodna jej f(x) = 3x³ jest równa zeru dla x = 0.

Przykład 2. Analogicznie funkcja

f(x)=x—sinx