0254

255

§ 1. Badanie przebiegu funkcji

5)    Wiadomo, że koszt eksploatacji statku w przeciągu godziny pływania wyraża się wzorem empirycznym a+bv³, gdzie a i b są stałymi, które powinny być obliczone dla każdego statku z osobna, zaś v jest prędkością statku w węzłach (węzeł =1,85 km/godz)(‘). Przy jakiej prędkości statek przebędzie dowolną odległość z najmniejszymi kosztami?

Na przebycie 1 km potrzeba 1/1,85 u godziny; odpowiednie koszty wyniosą

-(a+bv³)—-(bv*-\—^ •

l,85i>    1,85 \ o)

Przyrównując do zera pochodną wyrażenia y—bv²+alv otrzymamy y'_v=2bv—alv²=Q, skąd v = y/a/2b. Ponieważ y','i=2b+2alv³>0, koszty rzeczywiście osiągną najmniejszą wartość dla znalezionej wartości v.

Rys. 69

Przykład liczbowy: o=40, b=0,01, v = \J2000 * 12,6 (węzłów).

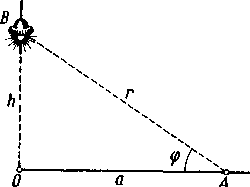
6)    Żarówka elektryczna może przesuwać się (na przykład na bloku) wzdłuż pionowej prostej OB (rys. 69). W jakiej odległości od płaszczyzny poziomej O A trzeba ją umieścić, żeby otrzymać w punkcie A tej płaszczyzny największe oświetlenie?

Wskazówka. Oświetlenie J jest wprost proporcjonalne do sin ę i odwrotnie proporcjonalne do kwadratu odległości r=AB, tj.

sin <p

J=c—₂- .

gdzie c zależy od siły światła żarówki.

Jeśli przyjąć jako zmienną niezależną h=OB, to

r=Jh² + a\

h

sin <p— — r

h

^J=C (h² + a³fⁱ

(0<A< +oo).

Pochodna

a-2h²

jest równa zeru dla h — al ^2x0,la zmieniając przy przejściu przez tę wartość znak ż plusa na minus. To jest właśnie najdogodniejsza odległość.

Można przyjąć jako zmienną niezależną kąt ę\ wtedy

a

cos <p

^c 2

J=~2 cos ę»sin q> a

i zadanie sprowadza się do znalezienia największej wartości funkcji y=cos² ęsin <p w przedziale (0, i n). Wiemy już jednak (patrz zadanie 3)), że wyrażenie to osiąga swą największą wartość dla kąta q>₀ spełniającego warunek tg ę₀ = 1/^/2. Dla odległości h otrzymamy poprzednią wartość a tg <p_a = aj

7) Z punktu A znajdującego się na magistrali kolejowej AB (rys. 70) kieruje się ładunki do punktu C znajdującego się w odległości CB—l od linii kolejowej. Koszt przewozu jednostki wagowej na jednostkę

(‘) W tym wzorze stała część kosztu a pochodzi od amortyzacji i kosztów utrzymania załogi, a drugi składnik bv³ od kosztu paliwa.