0278

279

§ 4. Obliczanie nieoznaczoności

Do funkcji /(1/f) i g(l/t) nowej zmiennej t można zastosować twierdzenie 3, co da nam

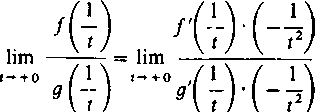
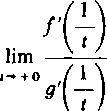
a wtedy również

.. m

lim--— K,

*- + « g(x)

cbdo.

Uwaga. Niekiedy przy obliczaniu wyrażeń nieoznaczonych rozpatrywanego typu można formalnie obejść się bez stosowania powyższych twierdzeń, wykorzystując rozwinięcie funkcji według wzoru Taylora [124- 125]. Niech x-»0 (zagadnienie zawsze można sprowadzić do tego przypadku). Jeśli z pomocą znanych rozwinięć uda się wydzielić z licznika i mianownika części główne

f(x) — axⁿ + o(x”),    g(x) = bx^m + o(x^m),

to jasne, jaka będzie granica ułamka f(x)/g(x). Równa się ona zeru, a/b, lub +oo, zależnie od tego czy rt jest większe, równe, czy też mniejsze od m (²). (Porównaj ustępy 62, 63).

Tak np. w przykładzie 1 zastępując funkcje e^x, e~^x i ln (e—x)— 1 =ln( 1—— J przez kilka pierwszych wyrazów ich rozwinięć otrzymujemy    '    ⁶

2e e— 1

(1+x +...) — (1— x+...)    2x+...

hm -_;---_;---=Jim *-o

Analogicznie w przykładzie 4:

x³ \    x³

= 2.

x+3+...J x ₃+-

lim ----r- = lim —;-

*ox

x—o / X

x-(x-- + ..

Proponujemy jako ćwiczenie rozwiązać tą metodą przykłady 3 i 5.

151. Wyrażenia nieoznaczone typu oo/oo. Zajmiemy się rozpatrzeniem wyrażeń nieoznaczonych typu oo/oo, tzn. zbadamy kwestię znajdowania granicy stosunku dwóch funkcji /(x) i g(x) dążących do nieskończoności (przy x->a).

0) Funkcje /(l/l) i    różniczkujemy względem t jako funkcje złożone.

(²) W ostatnim przypadku znak nieskończoności łatwo jest wyznaczyć na podstawie znaków a i b, jak również (w przypadku nieparzy stości różnicy m—n) na podstawie znaku x.