0305

306

V. Funkcje wielu zmiennych

(8_lt8₂,    , 8„>0), którego środkiem jest punkt M₀; najczęściej jest to kostka n-wy-

miarowa

(x?-«5,x° + <5;x°-<5,x° + <5;...;x„⁰-<5,x_B⁰ + <5)

(S> 0), której wszystkie wymiary są równe (=28).

2) Rozpatrzmy zbiór punktów M(x₁ ,x₂, ..., x_n), których współrzędne spełniają nierówności

x₁S¹0,    x₂>0..... x„^0, x₁ + x₂ + ...+x_n^h    (h>0).

Gdy n=2, obrazem geometrycznym odpowiadającym temu zbiorowi jest trójkąt równoramienny prostokątny, a dla n=2> — czworościan (rys. 95). W przypadku ogólnym

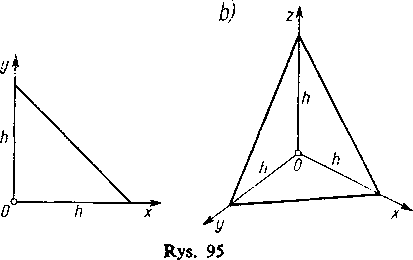
bryła ta nazywa się sympleksem (^Ł) domkniętym, w odróżnieniu od otwartego, który otrzymamy, jeśli w napisanych nierównościach wykluczymy równość.

3) Wreszcie zbiór punktów M(x_x, x₂, x_n) określony nierównością

(xi-x?)²+(x₂-x5)² + ... + (x_M-x°)²<r² (lub Kr²),

gdzie M₀(x°, x\, .... x„) jest punktem stałym, ar — stałą liczbą dodatnią, tworzy domkniętą (otwarty kulę n-wymiarową o promieniu r i środku w punkcie M₀. Innymi słowy kula jest zbiorem punktów M, których odległość od pewnego stałego punktu M₀ nie przewyższa r (lub jest mniejsza od r). Jest jasne samo przez się, że kuli takiej odpowiada dla n=2 koło (porównaj ustęp 150), a dla n=3 zwykła kula.

Kulę otwartą o dowolnym promieniu r>0 ze środkiem w punkcie M₀(x°_l, x₂, • • •, x°) można również rozpatrywać jako otoczenie tego punktu; w odróżnieniu od otoczenia prostopadłościennego, które wprowadziliśmy przedtem, to otoczenie będziemy nazywali kulistym.

Warto raz na zawsze zdać sobie sprawę z tego; że jeśli punkt M₀ znajduje się w otoczeniu jednego z dwóch wskazanych typów, to można umieścić go w otoczeniu drugiego typu i to tak, że to nowe otoczenie będzie zawarte w pierwszym otoczeniu.

1

Simplex znaczy po łacinie prosty, rzeczywiście, sympleks jest najprostszym wielościanem o najmniejszej możliwej w danej przestrzeni liczbie ścian.